Planet Musings

From the structure of the Standard Model of particle physics, one might wonder if the electron, muon and tau, so similar except for their masses, might really be the same object seen in three different guises. Last week, starting with a post for general readers, and then looking at the situation in more detail (Part 1 of this two-part series), I showed one way in which this idea fails to agree with experiment. Today I’ll give you another point of failure, focused on a property of particles known as “spin”.

Spin: The Idea In Brief

What is “spin” in physics? It’s related to the word “spin” in English, but with some adjustment. I’ll write a longer article about spin elsewhere, but here’s a brief introduction.

The Earth “spins”, both in the English sense and in the physics sense: it rotates. The same is true of a tennis ball. The rotation can be changed when the ball interacts with a tennis racket or with the ground. It can also be changed when it interacts with another tennis ball. In fact, if two balls strike each other, some of the spin of one ball can be transferred to the other, as in Fig. 1.

Elementary “particles” can have spin too, which can be (in part) changed by or transferred to other objects that they interact with. But this type of spin is somewhat different from ordinary rotation.

For example, an electron “spins”. Always. An interaction can change the direction of an electron’s spin, but it cannot change its overall amount. I’ll tell you what I mean by “amount” in a moment, but the quantity of the amount is a famous number:

• h / 4π = ℏ / 2

where h, Planck’s constant, shows up whenever quantum physics matters. This amount of spin is tiny; if a tennis ball had this amount of spin, it wouldn’t have even rotated once since the universe was born. But for an electron, it’s quite a lot.

Usually, as shorthand, one takes the ℏ to be implicit, and just says that “the electron has spin 1/2”. I’ll do that in what follows.

How can we visualize this spinning? It’s not easy. It’s best not to visualize an electron as a small rotating ball; it’s the wrong picture. Quantum field theory, the modern theory of “particles”, gives a different picture. Just as we should think of light as a wave made of wave-like photons, we should think of the electron as a wave — specifically, a wave in the electron field. [This wave is not to be confused with a wave function, which is something else]. A wave in the electron field can rotate in ways that a little ball cannot. This, however, is hard to draw, and in any case is a story for another day.

The important point is that the spin of an elementary “particle” is not like the simple rotational spinning of a tennis ball, even though it is in the same category. An electron has spin intrinsically, by its very nature; there is no electron without its spin, just as there is no electron without its internal energy and rest mass (as emphasized in my recent book, Chapter 17). That’s certainly not true for a tennis ball, which can have any spin, including none.

These details won’t matter much in what follows, though, so let’s step away from these subtleties and move on.

Ways to Spin

So far, I’ve suggested two types of spinning:

• the intrinsic spinning (or “intrinsic angular momentum”) of elementary particles
• the ordinary spinning (or “ordinary angular momentum”) of objects that are rotating, or are in orbit around other objects.

Both contribute to the surprising way that physicists use the word “spin”.

Suppose we have an object that is made of multiple elementary particles. Its total angular momentum involves combining the intrinsic angular momentum of its elementary particles with the ordinary angular momentum that the particles may have as they move around each other. Physicists now do something unexpected: they refer to the object’s total angular momentum as its spin. They do this even though the object is not elementary, meaning that its spin may potentially combine both intrinsic spinning and ordinary spinning of the objects inside it.

So the real meaning of spin, as particle physicists use the term, is this: it is the total angular momentum of an isolated object — an object that may be elementary, or that may itself be formed from multiple elementary objects. That means that the spin of an object like an atom, made of electrons, protons and neutrons, or of a proton, made of quarks, antiquarks and gluons, may potentially arise from multiple sources.

Atoms, Protons and Strings

For example, let’s take a hydrogen atom, made from an electron and a proton. (For starters we’ll treat both of these subatomic particles as though they were elementary. We’ll return to their possible internal structure later.)

I’ll refer in the following to four atomic states, illustrated below in Fig. 2.

• The ground state of a hydrogen atom (known as the “1s state”) has spin 0. Nevertheless, it is made of an electron with spin 1/2 surrounding a proton of spin 1/2. The two spin in opposite directions so that their angular momentum cancels.
  
• There is a very slightly excited state, often neglected in first-year physics courses or in quick summaries of atomic physics, where the electron and proton spin in the same direction, and their spins add instead of cancelling. This state of the atom has spin 1; I’ll call it the “spin-flipped 1s state”. (The transition from this excited state to the ground state involves the emission of a radio wave photon with a wavelength of 21 cm, leading to the so-called “21 cm line” widely observed in astronomy. )
  
• There are more dramatically excited states known as the “2s and 2p states”. The 2s state has spin 0, while the 2p state has spin 1. But even though the 2p state and the spin-flipped state both have spin 1, their spins have different origins. The total angular momentum of the 2p state does not come from the intrinsic angular momenta of the electron and proton; those cancel out, just as they do in the 1s and 2s states. Instead, the spin of the 2p state comes from a sort of rotational motion of the electron around the proton.

These four states are sketched in Figure 2. (Spin-flipped versions of the 2s and 2p states exist but are not shown.)

The fact that the ground state has spin 0, and yet the 2p state has larger spin specifically due to the electron’s motion around the proton, illustrates the main point of this post. If an object is made from multiple constituent objects, nothing can prevent those constituents from moving around one another. That means they can have ordinary (or “orbital”) angular momentum, which then contributes, along with the constituents’ spin, to the combined object’s spin — i.e., to its total angular momentum.

Therefore, an object that is not elementary, and so contains multiple objects inside it, will inevitably have excited states with different amounts of spin. Indeed, the hydrogen atom has excited states of total angular momentum 0, 1, 2, 3, and so on. All atoms exhibit similar behavior.

The same applies for protons, which aren’t elementary either. The proton has spin 1/2, but its excited states have spin 1/2, 3/2, 5/2, 7/2, and so on. The first excited state of the proton, the Delta, has spin 3/2. This is most easily understood as a rearrangement of the spins of the quarks, gluons and anti-quarks that it contains (though the exact rearrangement is not obvious, due to the complexity of a proton; see also chapter 6 of the book.) The next excited state, the p(1440), has spin 1/2 like the proton. But many other excited states have been observed, with spin 3/2, 5/2, 7/2, 9/2, and perhaps even 11/2.

A string, such as one finds in string theory, is another object with internal constituents, which one might call bits-of-string. A string can always be spun faster. That’s why, in the superstring theory that is sometimes touted as a potential “theory-of-everything” (or in less grandiose language, a complete theory of space, fields and particles), there are states of all possible spin — any integer times 1/2. Unfortunately, were this really the theory of our universe, the higher-spin states of the string would probably have far too much mass for us to make them in near-term experiments, putting this prediction of the theory out of reach for now.

But string theory isn’t just useful in this rarified context. It can also be used to describe the physics of “hadrons” — objects made from quarks and gluons, including protons. All indications from experiments and numerical calculations do indeed suggest that hadrons come in all possible spins; this includes the excited states of the proton already mentioned above. (That said, the higher the spin, the harder it is to make the states, making it more and more challenging to observe them.)

Spin and the Electron, Muon and Tau

None of this is true for electrons, muons or taus, all of which have spin 1/2. No electron-like particle with spin 3/2 has ever been observed.

This argues strongly against the electron, muon and tau all being made from the same object. Atoms, protons and strings all have excited states with the same spin as the ground state, but at roughly the same mass, they also have excited states with more spin. If the muon were an excited state of the electron, we would expect to see an object with spin 3/2 that has a mass comparable to the muon, and certainly below the mass of the tau. Such a state would easily have been observed decades ago, so it doesn’t exist.

Are there loopholes to this logic? Yes. It is possible, in special circumstances, for the excited states with higher spin to have much larger masses than the excited states which share the same spin as the ground state. This is a long story which I won’t try to tell here, but examples arises in the context of extra dimensions, and others in the related context of exotic theories of quark-like and gluon-like objects (with buzzwords such as “AdS/CFT” or “gauge/string duality”).

However, it’s hard to apply the loophole to the muon and tau. In such a scenario, the electron should have many more cousins than just two, and some of the others should have observed by now.

Furthermore, data now confirms that both the tau and muon get their rest mass from the Higgs field; see Fig. 3. For such particles, the loopholes I just mentioned don’t apply.

We must also recall the arguments given in the first part of this series. If muons and taus are excited states of electrons, it should be possible for any sufficiently energetic collision to turn an electron into a muon or tau, and for decays via photons to do the reverse. But these processes are not observed.

In short, the properties of the electron, muon and tau disfavor the idea that they are somehow secretly the same object in three different quantum states. The explanation of their similarities must lie elsewhere.

Three events coming up!

Tomorrow, Wednesday, May 15th, in the town of Northampton, Massachusetts, I’ll be speaking about my book — specifically, about why and how the relationship between ourselves and the universe is not what it seems. The event will be held at the Broadside Bookshop at 7pm. If you’re in the Pioneer Valley, please come by! And let your friends in the area know, too.

Since May 1st, Kris Brown, Nathaniel Osgood, Xiaoyan Li, William Waites and I have been meeting daily in James Clerk Maxwell’s childhood home in Edinburgh.

We’re hard at work on our project called New Mathematics and Software for Agent-Based models. It’s impossible to explain everything we’re doing while it’s happening. But I want to record some of our work. So please pardon how I skim through a bunch of already known ideas in my desperate attempt to quickly reach the main point. I’ll try to make up for this by giving lots of references.

Today I’ll talk about an interesting class of models we have developed together with Sean Wu. We call them ‘stochastic C-set rewriting systems’. They’re just part of our overall framework, but they’re an important part.

In this sort of model time is continuous, the state of the world is described by discrete data, and the state changes stochastically at discrete moments in time. All those features are already present in the class of models I described in Part 7. But today’s models are far more general, because the state of the world is described in a more general way! Now the state of the world at any moment of time is a C-set: a functor

for some fixed finitely presented category C to the category of sets.

C-sets are a flexible generalization of directed graphs. For example, a thing like this is a C-set for an appropriate choice of C:

There are also C-sets that look even less like graphs.

C-sets have been implemented in AlgebraicJulia, a software framework for doing scientific computation with categories. To learn more, start here:

• Evan Patterson, Graphs and C-sets I: What is a graph?, AlgebraicJulia Blog, 1 September 2020.

There’s a lot more on this blog explaining things you can do with C-sets, and how they’re implemented in AlgebraicJulia. We plan to take advantage of all this stuff!

In particular, we’ll use ‘double pushout rewriting’ to specify rules for how a C-set can change with time. If you’re not familiar with this concept, start here:

• nLab, Double pushout rewriting.

This concept is well-understood (by those who understand it well), so I’ll just roughly sketch it. In double pushout rewriting for C-sets, a rewrite rule is a diagram of C-sets

To apply this rewrite rule to a C-set S, we find inside that C-set an instance of the pattern L, called a ‘match’, and replace it with the pattern R. These ‘patterns’ are themselves C-sets. The C-set I can be thought of as the common part of L and I. The maps and tell us how this common part fits into L and R.

Note that in this incredibly sketchy explanation I am already starting to use maps between C-sets! Indeed, for each category C there’s a category called with:

• functors as objects: we call these C-sets;

• natural transformations between such functors as morphisms: we call these C-set maps.

This sort of category has been intensively studied for many decades, and there’s a huge amount we can do with them:

• nLab, Category of presheaves.

I used C-set maps in a couple of places above. First, the arrows here

are C-set maps. For slightly technical reasons we demand that be monic: that’s why I drew it with a hooked arrow. Second, I introduced the term ‘match’ without defining it. But we can define it: a match of L to a C-set S is simply a C-set map

And now for some good news: Kris Brown has already implemented double pushout rewriting for C-sets in AlgebraicJulia:

• Github, AlgebraicRewriting.jl.

Stochastic C-set rewriting systems

Now comes the main idea I want to explain.

A stochastic C-set rewriting system consists of:

1) a category C

2) a finite collection of rewrite rules

3) for each rewrite rule in our collection, a timer This is a stochastic map

That’s all.

What does this do for us? First, it means that for each choice of rewrite rule in our collection, and for each so-called start time we get a probability measure on

Let’s write to mean a randomly chosen element of distributed according to the probability measure We call the wait time, because it says how long after time we should wait until we apply the rewrite rule The time

is called the rewrite time.

In what follows, I’ll always assume these randomly chosen numbers are stochastically independent—even if we reuse the same timer repeatedly for different tasks.

Running a stochastic C-set rewriting system

Okay, so how do we actually use this for modeling? How do we ‘run’ a context-independent stochastic C-set rewriting system? I’ll sketch it out.

The idea is that at any time the state of the world is some C-set, say If you give me the initial state of the world the stochastic C-set rewriting system will tell you how to compute the state of the world at all later times. But this computation involves randomness.

Here’s how it works:

We start at We look for all matches to patterns in the initial state For each match we compute a wait time and then the rewrite time but right now We make a table of all the matches and their rewrite times.

The smallest of the rewrite times in our table, say is the first time the state of the world can change. We change it by applying the rewrite rule to the state of the world When we do this, we cross off the rewrite time and its corresponding match from our table.

More generally, suppose is any time when the state of the world changes. It will have changed by applying some rewrite rule to the previous state of the world, giving some new C-set

When this happens, new matches can appear, and existing matches can disappear. So we do this:

1) For each existing match that disappears, we cross off that match and its rewrite time from our table.

2) For each new match that appears, say one involving the rewrite rule we add that match and its rewrite time to our table.

We then wait until the smallest rewrite time in our table, say At that time, we apply the corresponding rewrite rule to the state , getting some new C-set We also cross off the rewrite time and its corresponding match from our table.

Then just keep doing the loop.

Subtleties

A lot of the subtleties in this formalism involve our use of timers.

For example, I computed wait times using a timer which is a stochastic map

The dependence on here means the wait time can depend on when we start the timer. And the fact that this stochastic map takes values in means the wait time can be infinite. This is a way of letting rewrite rules have a probability < 1 of ever being applied. If you don't like these features you can easily limit the formalism to avoid them.

The more serious subtleties involve whether and how to change wait times as the state of the world changes. For example, we can imagine more general timers that explicitly depend on the current state of the world as well as the time However, in this case I am confused about how we should update our table of wait times as the state of the world changes. So I decided to postpone discussing this generalization!

One day, early this spring, I found myself in a hotel elevator with three other people. The cohort consisted of two theoretical physicists, one computer scientist, and what appeared to be a normal person. I pressed the elevator’s 4 button, as my husband (the computer scientist) and I were staying on the hotel’s fourth floor. The button refused to light up.

“That happened last time,” the normal person remarked. He was staying on the fourth floor, too.

The other theoretical physicist pressed the 3 button.

“Should we press the 5 button,” the normal person continued, “and let gravity do its work?”

I took a moment to realize that he was suggesting we ascend to the fifth floor and then induce the elevator to fall under gravity’s influence to the fourth. We were reaching floor three, so I exchanged a “have a good evening” with the other physicist, who left. The door shut, and we began to ascend.

“As it happens,” I remarked, “he’s an expert on gravity.” The other physicist was Herman Verlinde, a professor at Princeton.

Such is a side effect of visiting the Simons Center for Geometry and Physics. The Simons Center graces the Stony Brook University campus, which was awash in daffodils and magnolia blossoms last month. The Simons Center derives its name from hedge-fund manager Jim Simons (who passed away during the writing of this article). He achieved landmark physics and math research before earning his fortune on Wall Street as a quant. Simons supported his early loves by funding the Simons Center and other scientific initiatives. The center reminded me of the Perimeter Institute for Theoretical Physics, down to the café’s linen napkins, so I felt at home.

I was participating in the Simons Center workshop “Entanglement, thermalization, and holography.” It united researchers from quantum information and computation, black-hole physics and string theory, quantum thermodynamics and many-body physics, and nuclear physics. We were to share our fields’ approaches to problems centered on thermalization, entanglement, quantum simulation, and the like. I presented about the eigenstate thermalization hypothesis, which elucidates how many-particle quantum systems thermalize. The hypothesis fails, I argued, if a system’s dynamics conserve quantities (analogous to energy and particle number) that can’t be measured simultaneously. Herman Verlinde discussed the ER=EPR conjecture.

My PhD advisor, John Preskill, blogged about ER=EPR almost exactly eleven years ago. Read his blog post for a detailed introduction. Briefly, ER=EPR posits an equivalence between wormholes and entanglement. 

The ER stands for Einstein–Rosen, as in Einstein–Rosen bridge. Sean Carroll provided the punchiest explanation I’ve heard of Einstein–Rosen bridges. He served as the scientific advisor for the 2011 film Thor. Sean suggested that the film feature a wormhole, a connection between two black holes. The filmmakers replied that wormholes were passé. So Sean suggested that the film feature an Einstein–Rosen bridge. “What’s an Einstein–Rosen bridge?” the filmmakers asked. “A wormhole.” So Thor features an Einstein–Rosen bridge.

EPR stands for Einstein–Podolsky–Rosen. The three authors published a quantum paradox in 1935. Their EPR paper galvanized the community’s understanding of entanglement.

ER=EPR is a conjecture that entanglement is closely related to wormholes. As Herman said during his talk, “You probably need entanglement to realize a wormhole.” Or any two maximally entangled particles are connected by a wormhole. The idea crystallized in a paper by Juan Maldacena and Lenny Susskind. They drew on work by Mark Van Raamsdonk (who masterminded the workshop behind this Quantum Frontiers post) and Brian Swingle (who’s appeared in further posts).

Herman presented four pieces of evidence for the conjecture, as you can hear in the video of his talk. One piece emerges from the AdS/CFT duality, a parallel between certain space-times (called anti–de Sitter, or AdS, spaces) and quantum theories that have a certain symmetry (called conformal field theories, or CFTs). A CFT, being quantum, can contain entanglement. One entangled state is called the thermofield double. Suppose that a quantum system is in a thermofield double and you discard half the system. The remaining half looks thermal—we can attribute a temperature to it. Evidence indicates that, if a CFT has a temperature, then it parallels an AdS space that contains a black hole. So entanglement appears connected to black holes via thermality and temperature.

Despite the evidence—and despite the eleven years since John’s publication of his blog post—ER=EPR remains a conjecture. Herman remarked, “It’s more like a slogan than anything else.” His talk’s abstract contains more hedging than a suburban yard. I appreciated the conscientiousness, a college acquaintance having once observed that I spoke carefully even over sandwiches with a friend.

A “source of uneasiness” about ER=EPR, to Herman, is measurability. We can’t check whether a quantum state is entangled via any single measurement. We have to prepare many identical copies of the state, measure the copies, and process the outcome statistics. In contrast, we seem able to conclude that a space-time is connected without measuring multiple copies of the space-time. We can check that a hotel’s first floor is connected to its fourth, for instance, by riding in an elevator once.

Or by riding an elevator to the fifth floor and descending by one story. My husband, the normal person, and I took the stairs instead of falling. The hotel fixed the elevator within a day or two, but who knows when we’ll fix on the truth value of ER=EPR?

With thanks to the conference organizers for their invitation, to the Simons Center for its hospitality, to Jim Simons for his generosity, and to the normal person for inspiration.

When I learned of Jim Simons’s passing, I was actually at the Simons Foundation headquarters in lower Manhattan, for the annual board meeting of the unparalleled Quanta Magazine, which Simons founded and named. The meeting was interrupted to share the sad news, before it became public … and then it was continued, because that’s obviously what Simons would’ve wanted. An oil portrait of Simons in the conference room took on new meaning.

See here for the Simons Foundation’s announcement, or here for the NYT’s obituary.

Although the Simons Foundation has had multiple significant influences on my life—funding my research, founding the Simons Institute for Theory of Computing in Berkeley that I often visit (including two weeks ago), and much more—I’ve exchanged all of a few sentences with Jim Simons himself. At a previous Simons Foundation meeting, I think he said he’d heard I’d moved from MIT to UT Austin, and asked whether I’d bought a cowboy hat yet. I said I did but I hadn’t yet worn it non-ironically, and he laughed at that. (My wife Dana knew him better, having spent a day at a brainstorming meeting for what became the Simons Institute, his trademark cigar smoke filling the room.)

I am, of course, in awe of what Jim Simons achieved in all three phases of his career — firstly, in mathematical research, where he introduced the Chern-Simons form and other pioneering contributions and led the math department at Stony Brook; secondly, in founding Renaissance and making insane amounts of money (“disproving the Efficient Market Hypothesis,” as some have claimed); and thirdly, in giving his money away to support basic research and the public understanding of it.

I’m glad that Simons, as a lifelong chain smoker, made it all the way to age 86. And I’m glad that the Simons Foundation, which I’m told will continue in perpetuity with no operational changes, will stand as a testament to his vision for the world.

If Hamlet had been a system of noncommuting charges, his famous soliloquy may have gone like this…

To thermalize, or not to thermalize, that is the question:
Whether ’tis more natural for the system to suffer
The large entanglement of thermalizing dynamics,
Or to take arms against the ETH
And by opposing inhibit it. To die—to thermalize,
No more; and by thermalization to say we end
The dynamical symmetries and quantum scars
That complicate dynamics: ’tis a consummation
Devoutly to be wish’d. To die, to thermalize;
To thermalize, perchance to compute—ay, there’s the rub:
For in that thermalization our quantum information decoheres,
When our coherence has shuffled off this quantum coil,
Must give us pause—there’s the respect
That makes calamity of resisting thermalization.

Hamlet (the quantum steampunk edition)

In the original play, Hamlet grapples with the dilemma of whether to live or die. Noncommuting charges have a dilemma regarding whether they facilitate or impede thermalization. Among the five research opportunities highlighted in the Perspective article, resolving this debate is my favourite opportunity due to its potential implications for quantum technologies. A primary obstacle in developing scalable quantum computers is mitigating decoherence; here, thermalization plays a crucial role. If systems with noncommuting charges are shown to resist thermalization, they may contribute to quantum technologies that are more resistant to decoherence. Systems with noncommuting charges, such as spin systems and squeezed states of light, naturally occur in quantum computing models like quantum dots and optical approaches. This possibility is further supported by recent advances demonstrating that non-Abelian symmetric operations are universal for quantum computing (see references 1 and 2).

In this penultimate blog post of the series, I will review some results that argue both in favour of and against noncommuting charges hindering thermalization. This discussion includes content from Sections III, IV, and V of the Perspective article, along with a dash of some related works at the end—one I recently posted and another I recently found. The results I will review do not directly contradict one another because they arise from different setups. My final blog post will delve into the remaining parts of the Perspective article.

Arguments for hindering thermalization

The first argument supporting the idea that noncommuting charges hinder thermalization is that they can reduce the production of thermodynamic entropy. In their study, Manzano, Parrondo, and Landi explore a collisional model involving two systems, each composed of numerous subsystems. In each “collision,” one subsystem from each system is randomly selected to “collide.” These subsystems undergo a unitary evolution during the collision and are subsequently returned to their original systems. The researchers derive a formula for the entropy production per collision within a certain regime (the linear-response regime). Notably, one term of this formula is negative if and only if the charges do not commute. Since thermodynamic entropy production is a hallmark of thermalization, this finding implies that systems with noncommuting charges may thermalize more slowly. Two other extensions support this result.

The second argument stems from an essential result in quantum computing. This result is that every algorithm you want to run on your quantum computer can be broken down into gates you run on one or two qubits (the building blocks of quantum computers). Marvian’s research reveals that this principle fails when dealing with charge-conserving unitaries. For instance, consider the charge as energy. Marvian’s results suggest that energy-preserving interactions between neighbouring qubits don’t suffice to construct all energy-preserving interactions across all qubits. The restrictions become more severe when dealing with noncommuting charges. Local interactions that preserve noncommuting charges impose stricter constraints on the system’s overall dynamics compared to commuting charges. These constraints could potentially reduce chaos, something that tends to lead to thermalization.

Adding to the evidence, we revisit the eigenstate thermalization hypothesis (ETH), which I discussed in my first post. The ETH essentially asserts that if an observable and Hamiltonian adhere to the ETH, the observable will thermalize. This means its expectation value stabilizes over time, aligning with the expectation value of the thermal state, albeit with some important corrections. Noncommuting charges cause all kinds of problems for the ETH, as detailed in these two posts by Nicole Yunger Halpern. Rather than reiterating Nicole’s succinct explanations, I’ll present the main takeaway: noncommuting charges undermine the ETH. This has led to the development of a non-Abelian version of the ETH by Murthy and collaborators. This new framework still predicts thermalization in many, but not all, cases. Under a reasonable physical assumption, the previously mentioned corrections to the ETH may be more substantial.

If this story ended here, I would have needed to reference a different Shakespearean work. Fortunately, the internal conflict inherent in noncommuting aligns well with Hamlet. Noncommuting charges appear to impede thermalization in various aspects, yet paradoxically, they also seem to promote it in others.

Arguments for promoting thermalization

Among the many factors accompanying the thermalization of quantum systems, entanglement is one of the most studied. Last year, I wrote a blog post explaining how my collaborators and I constructed analogous models that differ in whether their charges commute. One of the paper’s results was that the model with noncommuting charges had higher average entanglement entropy. As a result of that blog post, I was invited to CBC’s “Quirks & Quarks” Podcast to explain, on national radio, whether quantum entanglement can explain the extreme similarities we see in identical twins who are raised apart. Spoilers for the interview: it can’t, but wouldn’t it be grand if it could?

Following up on that work, my collaborators and I introduced noncommuting charges into monitored quantum circuits (MQCs)—quantum circuits with mid-circuit measurements. MQCs offer a practical framework for exploring how, for example, entanglement is affected by the interplay between unitary dynamics and measurements. MQCs with no charges or with commuting charges have a weakly entangled phase (“area-law” phase) when the measurements are done often enough, and a highly entangled phase (“volume-law” phase) otherwise. However, in MQCs with noncommuting charges, this weakly entangled phase never exists. In its place, there is a critical phase marked by long-range entanglement. This finding supports our earlier observation that noncommuting charges tend to increase entanglement.

I recently looked at a different angle to this thermalization puzzle. It’s well known that most quantum many-body systems thermalize; some don’t. In those that don’t, what effect do noncommuting charges have? One paper that answers this question is covered in the Perspective. Here, Potter and Vasseur study many-body localization (MBL). Imagine a chain of spins that are strongly interacting. We can add a disorder term, such as an external field whose magnitude varies across sites on this chain. If the disorder is sufficiently strong, the system “localizes.” This implies that if we measured the expectation value of some property of each qubit at some time, it would maintain that same value for a while. MBL is one type of behaviour that resists thermalization. Potter and Vasseur found that noncommuting charges destabilize MBL, thereby promoting thermalizing behaviour.

In addition to the papers discussed in our Perspective article, I want to highlight two other studies that study how systems can avoid thermalization. One mechanism is through the presence of “dynamical symmetries” (there are “spectrum-generating algebras” with a locality constraint). These are operators that act similarly to ladder operators for the Hamiltonian. For any observable that overlaps with these dynamical symmetries, the observable’s expectation value will continue to evolve over time and will not thermalize in accordance with the Eigenstate Thermalization Hypothesis (ETH). In my recent work, I demonstrate that noncommuting charges remove the non-thermalizing dynamics that emerge from dynamical symmetries.

Additionally, I came across a study by O’Dea, Burnell, Chandran, and Khemani, which proposes a method for constructing Hamiltonians that exhibit quantum scars. Quantum scars are unique eigenstates of the Hamiltonian that do not thermalize despite being surrounded by a spectrum of other eigenstates that do thermalize. Their approach involves creating a Hamiltonian with noncommuting charges and subsequently breaking the non-Abelian symmetry. When the symmetry is broken, quantum scars appear; however, if the non-Abelian symmetry were to be restored, the quantum scars vanish. These last three results suggest that noncommuting charges impede various types of non-thermalizing dynamics.

Unlike Hamlet, the narrative of noncommuting charges is still unfolding. I wish I could conclude with a dramatic finale akin to the duel between Hamlet and Laertes, Claudius’s poisoning, and the proclamation of a new heir to the Danish throne. However, that chapter is yet to be written. “To thermalize or not to thermalize?” We will just have to wait and see.

This post contains two unrelated announcements. Firstly, I would like to promote a useful list of resources for AI in Mathematics, that was initiated by Talia Ringer (with the crowdsourced assistance of many others) during the National Academies workshop on “AI in mathematical reasoning” last year. This list is now accepting new contributions, updates, or corrections; please feel free to submit them directly to the list (which I am helping Talia to edit). Incidentally, next week there will be a second followup webinar to the aforementioned workshop, building on the topics covered there. (The first webinar may be found here.)

Secondly, I would like to advertise the erdosproblems.com website, launched recently by Thomas Bloom. This is intended to be a living repository of the many mathematical problems proposed in various venues by Paul Erdős, who was particularly noted for his influential posing of such problems. For a tour of the site and an explanation of its purpose, I can recommend Thomas’s recent talk on this topic at a conference last week in honor of Timothy Gowers.

Thomas is currently issuing a call for help to develop the erdosproblems.com website in a number of ways (quoting directly from that page):

• You know Github and could set a suitable project up to allow people to contribute new problems (and corrections to old ones) to the database, and could help me maintain the Github project;
• You know things about web design and have suggestions for how this website could look or perform better;
• You know things about Python/Flask/HTML/SQL/whatever and want to help me code cool new features on the website;
• You know about accessibility and have an idea how I can make this website more accessible (to any group of people);
• You are a mathematician who has thought about some of the problems here and wants to write an expanded commentary for one of them, with lots of references, comparisons to other problems, and other miscellaneous insights (mathematician here is interpreted broadly, in that if you have thought about the problems on this site and are willing to write such a commentary you qualify);
• You knew Erdős and have any memories or personal correspondence concerning a particular problem;
• You have solved an Erdős problem and I’ll update the website accordingly (and apologies if you solved this problem some time ago);
• You have spotted a mistake, typo, or duplicate problem, or anything else that has confused you and I’ll correct things;
• You are a human being with an internet connection and want to volunteer a particular Erdős paper or problem list to go through and add new problems from (please let me know before you start, to avoid duplicate efforts);
• You have any other ideas or suggestions – there are probably lots of things I haven’t thought of, both in ways this site can be made better, and also what else could be done from this project. Please get in touch with any ideas!

I for instance contributed a problem to the site (#587) that Erdős himself gave to me personally (this was the topic of a somewhat well known photo of Paul and myself, and which he communicated again to be shortly afterwards on a postcard; links to both images can be found by following the above link). As it turns out, this particular problem was essentially solved in 2010 by Nguyen and Vu.

(Incidentally, I also spoke at the same conference that Thomas spoke at, on my recent work with Gowers, Green, and Manners; here is the video of my talk, and here are my slides.)

Unrelated Announcements: See here for a long interview with me in The Texas Orator, covering the usual stuff (quantum computing, complexity theory, AI safety). And see here for a podcast with me and Spencer Greenberg about a similar mix of topics.

A couple weeks ago, I helped organize UmeshFest: Don’t Miss This Flight, a workshop at UC Berkeley’s Simons Institute to celebrate the 2⁶th birthday of my former PhD adviser Umesh Vazirani. Peter Shor, John Preskill, Manuel Blum, Madhu Sudan, Sanjeev Arora, and dozens of other luminaries of quantum and classical computation were on hand to help tell the story of quantum computing theory and Umesh’s central role in it. There was also constant roasting of Umesh—of his life lessons from the squash court, his last-minute organizational changes and phone calls at random hours. I was delighted to find that my old coinage of “Umeshisms” was simply standard usage among the attendees.

At Berkeley, many things were as I remembered them—my favorite Thai eatery, the bubble tea, the Campanile—but not everything was the same. Here I am in front of Berkeley’s Gaza encampment, a.k.a. its “Anti Zionism Zone” or what was formerly Sproul Plaza (zoom into the chalk):

I felt a need to walk through the Anti Zionism Zone day after day (albeit unassumingly, neither draped in an Israeli flag nor looking to start an argument with anyone), for more-or-less the same reasons why the US regularly sends aircraft carriers through the Strait of Taiwan.

Back in the more sheltered environment of the Simons Institute, it was great to be among friends, some of whom I hadn’t seen since before Covid. Andris Ambainis and I worked together for a bit on an open problem in quantum query complexity, for old times’ sake (we haven’t solved it yet).

And then there were talks! I thought I’d share my own talk, which was entitled The Story of BQP (Bounded-Error Quantum Polynomial-Time). Here are the PowerPoint slides, but I’ll also share screen-grabs for those of you who constantly complain that you can’t open PPTX files.

I was particularly proud of the design of my title slide:

Moving on:

The class BQP/qpoly, I should explain, is all about an advisor who’s all-wise and perfectly benevolent, but who doesn’t have a lot of time to meet with his students, so he simply doles out the same generic advice to all of them, regardless of their thesis problem x.

I then displayed my infamous “Umeshisms” blog post from 2005—one of the first posts in the history of this blog:

As I explained, now that I hang out with the rationalist and AI safety communities, which are also headquartered in Berkeley, I’ve learned that my “Umeshisms” post somehow took on a life of its own. Once, when dining at one of the rationalists’ polyamorous Berkeley group houses, I said this has been lovely but I’ll now need to leave, to visit my PhD former adviser Umesh Vazirani. “You mean the Umesh?!” the rationalists excitedly exclaimed. “Of Umeshisms? If you’ve never missed a flight?”

But moving on:

(Note that by “QBPP,” Bethiaume and Brassard meant what we now call BQP.)

Feynman and Deutsch asked exactly the right question—does simulating quantum mechanics on a classical computer inherently produce an exponential slowdown, or not?—but they lacked most of the tools to start formally investigating the question. A factor-of-two quantum speedup for the XOR function could be dismissed as unimpressive, while a much greater quantum speedup for the “constant vs. balanced” problem could be dismissed as a win against only deterministic classical algorithms, rather than randomized algorithms. Deutsch-Jozsa may have been the first time that an apparent quantum speedup faltered in an honest comparison against classical algorithms. It certainly wasn’t the last!

Ah, but this is where Bernstein and Vazirani enter the scene.

Bernstein and Vazirani didn’t merely define BQP, which remains the central object of study in quantum complexity theory. They also established its most basic properties:

And, at least in the black-box model, Bernstein and Vazirani gave the first impressive quantum speedup for a classical problem that survived in a fair comparison against the best classical algorithm:

The Recursive Bernstein-Vazirani problem, also called Recursive Fourier Sampling, is constructed as a “tree” of instances of the Bernstein-Vazirani problem, where to query the Boolean function at any given level, you need to solve a Bernstein-Vazirani problem for a Boolean function at the level below it, and then run the secret string s through a fixed Boolean function g. For more, see my old paper Quantum Lower Bound for Recursive Fourier Sampling.

Each Bernstein-Vazirani instance has classical query complexity n and quantum query complexity 1. So, if the tree of instances has depth d, then overall the classical query complexity is n^d, while the quantum query complexity is only 2^d. Where did the 2 come from? From the need to uncompute the secret strings s at each level, to enable quantum interference at the next level up—thereby forcing us to run the algorithm twice. A key insight.

The Recursive Fourier Sampling separation set the stage for Simon’s algorithm, which gave a more impressive speedup in the black-box model, and thence for the famous Shor’s algorithm for factoring and discrete log:

But Umesh wasn’t done establishing the most fundamental properties of BQP! There’s also the seminal 1994 paper by Bennett, Bernstein, Brassard, and Vazirani:

In light of the BV and BBBV papers, let’s see how BQP seems to fit with classical complexity classes—an understanding that’s remained largely stable for the past 30 years:

We can state a large fraction of the research agenda of the whole field, to this day, as questions about BQP:

I won’t have time to discuss all of these questions, but let me at least drill down on the first few.

Many people hoped the list of known problems in BQP would now be longer than it is. So it goes: we don’t decide the truth, we only discover it.

As a 17-year-old just learning about quantum computing in 1998 by reading the Bernstein-Vazirani paper, I was thrilled when I managed to improve their containment BQP ⊆ P^#P to BQP ⊆ PP. I thought that would be my big debut in quantum complexity theory. I was then crushed when I learned that Adleman, DeMarrais, and Huang had proved the same thing a year prior. OK, but at least it wasn’t, like, 50 years prior! Maybe if I kept at it, I’d reach the frontier soon enough.

Umesh, from the very beginning, raised the profound question of BQP’s relation to the polynomial hierarchy. Could we at least construct an oracle relative to which BQP⊄PH—or, closely related, relative to which P=NP≠BQP? Recursive Fourier Sampling was a already candidate for such a separation. I spent months trying to prove that candidate wasn’t in PH, but failed. That led me eventually to propose a very different problem, Forrelation, which seemed like a stronger candidate, although I couldn’t prove that either. Finally, in 2018, after four years of effort, Ran Raz and Avishay Tal proved that my Forrelation problem was not in PH, thereby resolving Umesh’s question after a quarter century.

We now know three different ways by which a quantum computer can not merely solve any BQP problem efficiently, but prove its answer to a classical skeptic via an interactive protocol! Using quantum communication, using two entangled (but non-communicating) quantum computers, or using cryptography (this last a breakthrough of Umesh’s PhD student Urmila Mahadev). It remains a great open problem, first posed to my knowledge by Daniel Gottesman, whether one can do it with none of these things.

To see many of the advantages of quantum computation over classical, we’ve learned that we need to broaden our vision beyond BQP (which is a class of languages), to promise problems (like estimating the expectation values of observables), sampling problems (like BosonSampling and Random Circuit Sampling), and relational problems (like the Yamakawa-Zhandry problem, subject of a recent breakthrough). It’s conceivable that quantum advantage could remain for such problems even if it turned out that P=BQP.

A much broader question is whether BQP captures all languages that can be efficiently decided using “reasonable physical resources.” What about chiral quantum field theories, like the Standard Model of elementary particles? What about quantum theories of gravity? Good questions!

Since it was Passover during the talk, I literally said “Dayenu” to Umesh: “if you had only given us BQP, that would’ve been enough! but you didn’t, you gave us so much more!”

Happy birthday Umesh!! We look forward to celebrating again on all your subsequent power-of-2 birthdays.

[UPDATE May 10, 4:00 pm Boston Time, 10:00 pm EU time: AURORAS MAY BE ACTIVE NOW!]

I don’t use exclamation marks in blog post titles lightly. For those of us hoping to see the northern and southern lights (auroras) outside their usual habitat near the Earth’s poles, this is one of those rare weekends where the odds are in our favor. NOAA’s Space Weather Prediction Center has issued a rare G4 forecast (out of a range from G1 to G5) for a major geomagnetic “storm”.

Though the large and active sunspot from earlier this week has moved on, it has been followed by an even larger group of sunspots, so enormous that you can easily see them with eclipse glasses if you’ve kept your pair from last month.

Powerful solar flares (explosions at the Sun’s visible surface) and the accompanying large coronal mass ejections (“CMEs”, huge clouds of subatomic particles that stream across space from the Sun toward the planets) keep coming, one after another; the second-largest of the week happened just a few hours ago. In the next 24-72 hours, the combined effects of these CMEs may drive the Earth’s magnetic field haywire, leading to northern and southern lights that are much stronger and much more equatorial than usual.

This picture by Roice Nelson shows a remarkable structure: the hexagonal tiling honeycomb.

What is it? Roughly speaking, a honeycomb is a way of filling 3d space with polyhedra. The most symmetrical honeycombs are the ‘regular’ ones. For any honeycomb, we define a flag to be a chosen vertex lying on a chosen edge lying on a chosen face lying on a chosen polyhedron. A honeycomb is regular if its geometrical symmetries act transitively on flags.

The most familiar regular honeycomb is the usual way of filling Euclidean space with cubes. This cubic honeycomb is denoted by the symbol {4,3,4}, because a square has 4 edges, 3 squares meet at each corner of a cube, and 4 cubes meet along each edge of this honeycomb. We can also define regular honeycombs in hyperbolic space. For example, the order-5 cubic honeycomb is a hyperbolic honeycomb denoted {4,3,5}, since 5 cubes meet along each edge:

Coxeter showed there are 15 regular hyperbolic honeycombs. The hexagonal tiling honeycomb is one of these. But it does not contain polyhedra of the usual sort! Instead, it contains flat Euclidean planes embedded in hyperbolic space, each plane containing the vertices of infinitely many regular hexagons. You can think of such a sheet of hexagons as a generalized polyhedron with infinitely many faces. You can see a bunch of such sheets in the picture:

The symbol for the hexagonal tiling honeycomb is {6,3,3}, because a hexagon has 6 edges, 3 hexagons meet at each corner in a plane tiled by regular hexagons, and 3 such planes meet along each edge of this honeycomb. You can see that too if you look carefully.

A flat Euclidean plane in hyperbolic space is called a horosphere. Here’s a picture of a horosphere tiled with regular hexagons, yet again drawn by Roice:

Unlike the previous pictures, which are views from inside hyperbolic space, this uses the Poincaré ball model of hyperbolic space. As you can see here, a horosphere is a limiting case of a sphere in hyperbolic space, where one point of the sphere has become a ‘point at infinity’.

Be careful. A horosphere is intrinsically flat, so if you draw regular hexagons on it their internal angles are

as usual in Euclidean geometry. But a horosphere is not ‘totally geodesic’: straight lines in the horosphere are not geodesics in hyperbolic space! Thus, a hexagon in hyperbolic space with the same vertices as one of the hexagons in the horosphere actually bulges out from the horosphere a bit — and its internal angles are less than : they are

This angle may be familar if you’ve studied tetrahedra. That’s because each vertex lies at the center of a regular tetrahedron, with its four nearest neighbors forming the tetrahedron’s corners.

It’s really these hexagons in hyperbolic space that are faces of the hexagonal tiling honeycomb, not those tiling the horospheres, though perhaps you can barely see the difference. This can be quite confusing until you think about a simpler example, like the difference between a cube in Euclidean 3-space and a cube drawn on a sphere in Euclidean space.

Connection to special relativity

There’s an interesting connection between hyperbolic space, special relativity, and 2×2 matrices. You see, in special relativity, Minkowski spacetime is equipped with the nondegenerate bilinear form

usually called the Minkowski metric. Hyperbolic space sits inside Minowski spacetime as the hyperboloid of points with and But we can also think of Minkowski spacetime as the space of 2×2 hermitian matrices, using the fact that every such matrix is of the form

and

In these terms, the future cone in Minkowski spacetime is the cone of positive definite hermitian matrices:

Sitting inside this we have the hyperboloid

which is none other than hyperbolic space!

Connection to the Eisenstein integers

Since the hexagonal tiling honeycomb lives inside hyperbolic space, which in turn lives inside Minkowski spacetime, we should be able to describe the hexagonal tiling honeycomb as sitting inside Minkowski spacetime. But how?

Back in 2022, James Dolan and I conjectured such a description, which takes advantage of the picture of Minkowski spacetime in terms of 2×2 matrices. And this April, working on Mathstodon, Greg Egan and I proved this conjecture!

I’ll just describe the basic idea here, and refer you elsewhere for details.

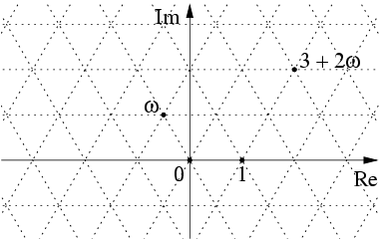
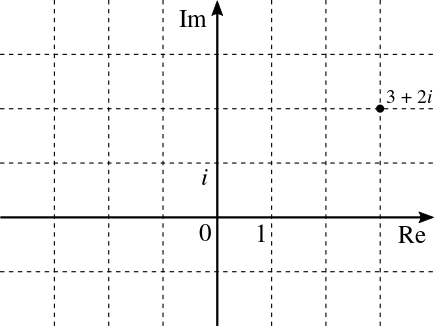
The Eisenstein integers are the complex numbers of the form

where and are integers and is a cube root of 1. The Eisenstein integers are closed under addition, subtraction and multiplication, and they form a lattice in the complex numbers:

Similarly, the set of 2×2 hermitian matrices with Eisenstein integer entries gives a lattice in Minkowski spacetime, since we can describe Minkowski spacetime as

Here’s the conjecture:

Conjecture. The points in the lattice that lie on the hyperboloid are the centers of hexagons in a hexagonal tiling honeycomb.

Using known results, it’s relatively easy to show that there’s a hexagonal tiling honeycomb whose hexagon centers are all points in The hard part is showing that every point in is a hexagon center. Points in are the same as 4-tuples of integers obeying an inequality (the condition) and a quadratic equation (the condition). So, we’re trying to show that all 4-tuples obeying those constraints follow a very regular pattern.

Here are two proofs of the conjecture:

• John Baez, Line bundles on complex tori (part 5), The n-Category Café, April 30, 2024.

Greg Egan and I came up with the first proof. The basic idea was to assume there’s a point in that’s not a hexagon center, choose one as close as possible to the identity matrix, and then construct an even closer one, getting a contradiction. Shortly thereafter, someone on Mastodon by the name of Mist came up with a second proof, similar in strategy but different in detail. This increased my confidence in the result.

What’s next?

Something very similar should be true for another regular hyperbolic honeycomb, the square tiling honeycomb:

Here instead of the Eisenstein integers we should use the Gaussian integers, , consisting of all complex numbers

where and are integers.

Conjecture. The points in the lattice that lie on the hyperboloid are the centers of squares in a square tiling honeycomb.

I’m also very interested in how these results connect to algebraic geometry! I explained this in some detail here:

• Line bundles on complex tori (part 4), The n-Category Café, April 26, 2024.

Briefly, the hexagon centers in the hexagonal tiling honeycomb correspond to principal polarizations of the abelian variety . These are concepts that algebraic geometers know and love. Similarly, if the conjecture above is true, the square centers in the square tiling honeycomb will correspond to principal polarizations of the abelian variety . But I’m especially interested in interpreting the other features of these honeycombs — not just the hexagon and square centers — using ideas from algebraic geometry.

With all the hype around machine learning, I occasionally get asked if it could be used to make predictions for particle colliders, like the LHC.

Physicists do use machine learning these days, to be clear. There are tricks and heuristics, ways to quickly classify different particle collisions and speed up computation. But if you’re imagining something that replaces particle physics calculations entirely, or even replace the LHC itself, then you’re misunderstanding what particle physics calculations are for.

Why do physicists try to predict the results of particle collisions? Why not just observe what happens?

Physicists make predictions not in order to know what will happen in advance, but to compare those predictions to experimental results. If the predictions match the experiments, that supports existing theories like the Standard Model. If they don’t, then a new theory might be needed.

Those predictions certainly don’t need to be made by humans: most of the calculations are done by computers anyway. And they don’t need to be perfectly accurate: in particle physics, every calculation is an approximation. But the approximations used in particle physics are controlled approximations. Physicists keep track of what assumptions they make, and how they might go wrong. That’s not something you can typically do in machine learning, where you might train a neural network with millions of parameters. The whole point is to be able to check experiments against a known theory, and we can’t do that if we don’t know whether our calculation actually respects the theory.

That difference, between caring about the result and caring about how you got there, is a useful guide. If you want to predict how a protein folds in order to understand what it does in a cell, then you will find AlphaFold useful. If you want to confirm your theory of how protein folding happens, it will be less useful.

Some industries just want the final result, and can benefit from machine learning. If you want to know what your customers will buy, or which suppliers are cheating you, or whether your warehouse is moldy, then machine learning can be really helpful.

Other industries are trying, like particle physicists, to confirm that a theory is true. If you’re running a clinical trial, you want to be crystal clear about how the trial data turn into statistics. You, and the regulators, care about how you got there, not just about what answer you got. The same can be true for banks: if laws tell you you aren’t allowed to discriminate against certain kinds of customers for loans, you need to use a method where you know what traits you’re actually discriminating against.

So will physicists use machine learning? Yes, and more of it over time. But will they use it to replace normal calculations, or replace the LHC? No, that would be missing the point.

A couple of days ago, I noted a chance of auroras (a.k.a. northern and southern lights) this week. That chance just went up again, with a series of solar flares and coronal mass ejections. The chance of auroras being visible well away from their usual latitudes is pretty high in the 36-48 hour range… meaning the evening of May 10th into the morning of May 11th in both Europe (with the best chances) and in the US and Canada.

Keep in mind that timing and aurora strength are hard to predict, so no prediction is guaranteed; it could come to nothing, or the auroras could show up somewhat earlier and be stronger than expected.

Meanwhile, the SciComm 2 conference continues at the Perimeter Institute. As part of it, experimental particle physicist Clara Nellist gave a public talk to an enthusiastic audience last night, reviewing the LHC experiments and their achievements. You can find it on YouTube if you’d like to watch it.

I’ll be spending the remainder of this week at the 2nd Scicomm Collider conference, hosted at the Perimeter Institute in Waterloo, Ontario, and organized by astrophysicist and writer Katie Mack. I’m very much looking forward to it!

Next week I’ll be back in Massachusetts, in the town of Northampton, where I’ll be speaking about my book. The event is at 7pm on Wednesday, May 15th at the lovely Broadside Bookshop. If you’re in the Pioneer Valley, please join me! And if you have friends in the area, please let them know.

Carbon nanotubes are one of the most elastically strong materials out there.  A bit over a decade ago, a group at Michigan State did a serious theoretical analysis of how much energy you could store in a twisted yarn made from single-walled carbon nanotubes.  They found that the specific energy storage could get as large as several MJ/kg, as much as four times what you get with lithium ion batteries!

Now, a group in Japan has actually put this to the test, in this Nature Nano paper.  They get up to 2.1 MJ/kg, over the lithium ion battery mark, and the specific power (when they release the energy) at about \(10^{6}\) W/kg is not too far away from "non-cyclable" energy storage media, like TNT.  Very cool!  

read more

Last time I introduced a 2-dimensional complex variety called the Eisenstein surface

$$E = \mathbb{C}/\mathbb{E} \times \mathbb{C}/\mathbb{E}$$

where $\mathbb{E} \subset \mathbb{C}$ is the lattice of Eisenstein integers. We worked out the Néron–Severi group $\mathrm{NS}(E)$ of this surface: that is, the group of equivalence classes of holomorphic line bundles on this surface, where we count two as equivalent if they’re isomorphic as topological line bundles. And we got a nice answer:

$$\mathrm{NS}(E) \cong \mathfrak{h}_2(\mathbb{E})$$

where $\mathfrak{h}_2(\mathbb{E})$ consists of $2 \times 2$ hermitian matrices with Eisenstein integers as entries.

Now we’ll see how this is related to the ‘hexagonal tiling honeycomb’:

We’ll see an explicit bijection between so-called ‘principal polarizations’ of the Eisenstein surface and the centers of hexagons in this picture! We won’t prove it works — I hope to do that later. But we’ll get everything set up.

The hexagonal tiling honeycomb

This picture by Roice Nelson shows a remarkable structure: the hexagonal tiling honeycomb.

What is it? Roughly speaking, a honeycomb is a way of filling 3d space with polyhedra. The most symmetrical honeycombs are the ‘regular’ ones. For any honeycomb, we define a flag to be a chosen vertex lying on a chosen edge lying on a chosen face lying on a chosen polyhedron. A honeycomb is regular if its geometrical symmetries act transitively on flags.

The most familiar regular honeycomb is the usual way of filling Euclidean space with cubes. This cubic honeycomb is denoted by the symbol $\{4,3,4\}$, because a square has 4 edges, 3 squares meet at each corner of a cube, and 4 cubes meet along each edge of this honeycomb. We can also define regular honeycombs in hyperbolic space. For example, the order-5 cubic honeycomb is a hyperbolic honeycomb denoted $\{4,3,5\}$, since 5 cubes meet along each edge:

Coxeter showed there are 15 regular hyperbolic honeycombs. The hexagonal tiling honeycomb is one of these. But it does not contain polyhedra of the usual sort! Instead, it contains flat Euclidean planes embedded in hyperbolic space, each plane containing the vertices of infinitely many regular hexagons. You can think of such a sheet of hexagons as a generalized polyhedron with infinitely many faces. You can see a bunch of such sheets in the picture:

The symbol for the hexagonal tiling honeycomb is $\{6,3,3\}$, because a hexagon has 6 edges, 3 hexagons meet at each corner in a plane tiled by regular hexagons, and 3 such planes meet along each edge of this honeycomb. You can see that too if you look carefully.

A flat Euclidean plane in hyperbolic space is called a horosphere. Here’s a picture of a horosphere tiled with regular hexagons, yet again drawn by Roice:

Unlike the previous pictures, which are views from inside hyperbolic space, this uses the Poincaré ball model of hyperbolic space. As you can see here, a horosphere is a limiting case of a sphere in hyperbolic space, where one point of the sphere has become a ‘point at infinity’.

Be careful. A horosphere is intrinsically flat, so if you draw regular hexagons on it their internal angles are

$$2\pi/3 = 120^\circ$$

as usual in Euclidean geometry. But a horosphere is not ‘totally geodesic’: straight lines in the horosphere are not geodesics in hyperbolic space! Thus, a hexagon in hyperbolic space with the same vertices as one of the hexagons in the horosphere actually bulges out from the horosphere a bit — and its internal angles are less than $2\pi/3$: they are

$$\arccos\left(-\frac{1}{3}\right) \approx 109.47^\circ$$

It’s really these hexagons in hyperbolic space that are faces of the hexagonal tiling honeycomb, not those tiling the horospheres, though perhaps you can barely see the difference. This can be quite confusing until you think about a simpler example, like the difference between a cube in Euclidean 3-space and a cube drawn on a sphere in Euclidean space.

Connection to special relativity

Johnson and Weiss have studied the symmetry group of the hexagonal tiling honeycomb:

• Norman W. Johnson and Asia Ivic Weiss, Quadratic integers and Coxeter groups, Canad. J.Math. 51 (1999), 1307–1336.

They describe this group using the ring of Eisenstein integers:

$$\mathbb{E} = \{ a + b \omega \; \vert \; a, b \in \mathbb{Z} \} \subset \mathbb{C}$$

where $\omega$ is the cube root of unity $\exp(2 \pi i/ 3)$. And I believe their work implies this result:

Theorem. The orientation-preserving symmetries of the hexagonal tiling honeycomb form the group $\mathrm{PGL}(2,\mathbb{E})$.

I’ll sketch a proof later, starting from what they actually show.

For comparison, the group of all orientation-preserving symmetries of hyperbolic space forms the larger group $\mathrm{PGL}(2,\mathbb{C})$. This group is the same as $\mathrm{PSL}(2,\mathbb{C})$… and this naturally brings Minkowski spacetime into the picture!

You see, in special relativity, Minkowski spacetime is $\mathbb{R}^4$ equipped with the nondegenerate bilinear form

$$(t,x,y,z) \cdot (t',x',y',z') = t t' - x x' - y y' - z z$$

usually called the Minkowski metric.

Hyperbolic space sits inside Minowski spacetime as the hyperboloid of points $\mathbf{x} = (t,x,y,z)$ with $\mathbf{x} \cdot \mathbf{x} = 1$ and $t &gt; 0$. Equivalently, we can think of Minkowski spacetime as the space $\mathfrak{h}_2(\mathbb{C})$ of $2 \times 2$ hermitian complex matrices, using the fact that every such matrix is of the form

$$A = \left( \begin{array}{cc} t + z & x - i y \\ x + i y & t - z \end{array} \right)$$

and

$$\det(A) = t^2 - x^2 - y^2 - z^2$$

One reason this viewpoint is productive is that the group of symmetries of Minkowski spacetime that preserve the orientation and also preserve the distinction between future and past is the projective special linear group $\mathrm{PSL}(2,\mathbb{C})$. The idea here is that any element $g \in \mathrm{SL}(2,\mathbb{C})$ acts on $\mathfrak{h}_2(\mathbb{C})$ by

$$A \mapsto g A g^\ast$$

This action clearly preserves the Minkowski metric (since it preserves the determinant of $A$) and also the orientation and the direction of time (because $\mathrm{SL}(2,\mathbb{C})$ is connected). However, multiples of the identity matrix, namely the matrices $\pm I$, act trivially. So, we get an action of the quotient group $\mathrm{PSL}(2,\mathbb{C})$.

In these terms, the future cone in Minkowski spacetime is the cone of positive definite hermitian matrices:

$$\mathcal{K} = \left\{A \in \mathfrak{h}_2(\mathbb{C}) \, \vert \, \det A &gt; 0, \, \mathrm{tr}(A) &gt; 0 \right\}$$

Sitting inside this we have the hyperboloid

$$\mathcal{H} = \left\{A \in \mathfrak{h}_2(\mathbb{C}) \, \vert \, \det A = 1, \, \mathrm{tr}(A) &gt; 0 \right\}$$

which is none other than hyperbolic space! The Minkowski metric on $\mathfrak{h}_2(\mathbb{C})$ induces the usual Riemannian metric on hyperbolic space (up to a change of sign).

Indeed, not only is the symmetry group of the hexagonal tiling honeycomb abstractly isomorphic to the subgroup

$$\mathrm{PGL}(2,\mathbb{E}) \subset \mathrm{PGL}(2,\mathbb{C}) = \mathrm{PSL}(2,\mathbb{C})$$

we’ve also seen this subgroup acts as orientation-preserving isometries of hyperbolic space. So it seems almost obvious that $\mathrm{PGL}(2,\mathbb{E})$ acts on hyperbolic space so as to preserve some hexagonal tiling honeycomb!

Constructing the hexagonal tiling honeycomb

Thus, the big question is: how can we actually construct a hexagonal tiling honeycomb inside $\mathcal{H}$ that is preserved by the action of $\mathrm{PGL}(2,\mathbb{E})$? I want to answer this question.

Sitting in the complex numbers we have the ring $\mathbb{E}$ of Eisenstein integers. This lets us define a lattice in Minkowski spacetime, called $\mathfrak{h}_2(\mathbb{E})$, consisting of $2 \times 2$ hermitian matrices with entries that are Eisenstein integers. James Dolan and I conjectured this:

Conjecture. The points in the lattice $\mathfrak{h}_2(\mathbb{E})$ that lie on the hyperboloid $\mathcal{H}$ are the centers of hexagons in a hexagonal tiling honeycomb.

I think Greg Egan has done enough work to make this clear. I will try to write up proof here next time. Once this is done, it should be fairly easy to construct the other features of the hexagonal tiling honeycomb. They should all be related in various ways to the lattice $\mathfrak{h}_2(\mathbb{E})$.

Connection to the Néron–Severi group of the Eisenstein surface

But what does any of this have to do with the supposed theme of these blog posts: line bundles on complex tori? To answer this, we need to remember that last time I gave an explicit isomorphism between

• the Néron–Severi group $\mathrm{NS}(E)$ of the Eisenstein surface $E = \mathbb{C}^2/\mathbb{E}^2$

and

• $\mathfrak{h}_2(\mathbb{E})$ (viewed as an additive group).

This isomorphism wasn’t new: experts know a lot about it. For example, under this correspondence, elements $A \in \mathfrak{h}_2(\mathbb{E})$ with $\det(A) &gt; 0$ and $\mathrm{tr}(A) &gt; 0$ correspond to elements of the Néron–Severi group coming from ample line bundles. Elements of the Néron–Severi group coming from ample line bundles are called polarizations.

Furthermore, elements with $A \in \mathfrak{h}_2(\mathbb{E})$ with $\det(A) = 1$ and $\mathrm{tr}(A) &gt; 0$ are known to correspond to certain specially nice polarizations called ‘principal’ polarizations.

So, the conjecture implies this:

Main Result. There is an explicit bijection between principal polarizations of the Eisenstein surface and centers of hexagons in the hexagonal tiling honeycomb.

There’s a lot more to say, but I’ll stop here for now, at least after filling in some details that I owe you.

Symmetries of the hexagonal tiling honeycomb

As shown already by Coxeter, the group of all isometries of hyperbolic space mapping the hexagonal tiling honeycomb to itself is the Coxeter group $[6,3,3]$. That means this group has a presentation with generators $v, e, f, p$ and relations

$$v^2 = e^2 = f^2 = p^2 = 1$$

$$(v e)^6 = 1, \qquad (e f)^3 = 1, \qquad (f p)^3 = 1, \qquad (v f)^2 = 1, \qquad (e p)^2 = 1$$

Each generator corresponds to a reflection in hyperbolic space — that is, an orientation-reversing transformation that preserves angles and distances. The products of pairs of generators are orientation preserving, and they generate an index-2 subgroup of $[6,3,3]$ called $[6,3,3]^+$.

Johnson and Weiss describe the group $[6,3,3]^+$ using the Eisenstein integers. Namely, they show it’s isomorphic to the group $\mathrm{P}\overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E})$.

But what the heck is that?

As usual, $\mathrm{SL}(2,\mathbb{E})$ is the group of $2 \times 2$ matrices with entries in $\mathbb{E}$ having determinant $1$. But Johnson and Weiss define a slightly larger group $\overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E})$ to consist of all $2 \times 2$ matrices with entries in $\mathbb{E}$ that have determinant with absolute value $1$. This in turn has a subgroup $\overline{\mathrm{S}}\mathrm{Z}(2,\mathbb{E})$ consisting of multiples of the identity $\lambda I$ where $\lambda \in \mathbb{E}$ has absolute value $1$. Then they define $\mathrm{P}\overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E}) = \overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E})/\overline{\mathrm{S}}\mathrm{Z}(2,\mathbb{E})$.

What does the group $\mathrm{P}\overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E})$ actually amount to? Since all the units in $\mathbb{E}$ have absolute value $1$ — they’re just the 6th roots of unity — $\overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E})$ is the same as the group $\mathrm{GL}(2,\mathbb{E})$ consisting of all invertible $2 \times 2$ matrices with entries in $\mathbb{E}$. The subgroup $\overline{\mathrm{S}}\mathrm{Z}(2,\mathbb{E})$ consists of matrices $\lambda I$ where $\lambda$ is a 6th root of unity. If I’m not confused, this is just the center of $\mathrm{GL}(2,\mathbb{E})$. So what they’re calling $\mathrm{P}\overline{\mathrm{S}}\mathrm{L}(2,\mathbb{E})$ is $\mathrm{GL}(2,\mathbb{E})$ modulo its center. This is usually called $\mathrm{PGL}(2,\mathbb{E})$.

All this is a bit confusing, but I think that with massive help from Johnson and Weiss we’ve shown this:

Theorem. The orientation-preserving symmetries of the hexagonal tiling honeycomb form the group $\mathrm{PGL}(2,\mathbb{E})$.

The interplay between $\mathrm{PSL}(2,\mathbb{E})$ and $\mathrm{PGL}(2,\mathbb{E})$ will become clearer next time: the latter group contains some 60 degree rotations that the former group does not!

The Eisenstein integers $\mathbb{E}$ are the complex numbers of the form $a + b \omega$ where $a$ and $b$ are integers and $\omega = \exp(2 \pi i/3)$. They form a subring of the complex numbers and also a lattice:

Last time I explained how the space $\mathfrak{h}_2(\mathbb{C})$ of $2 \times 2$ hermitian matrices is secretly 4-dimensional Minkowski spacetime, while the subset

$$\mathcal{H} = \left\{A \in \h_2(\mathbb{C}) \, \vert \, \det A = 1, \, \mathrm{tr}(A) \gt 0 \right\}$$

is 3-dimensional hyperbolic space. Thus, the set $\mathfrak{h}_2(\mathbb{E})$ of $2 \times 2$ hermitian matrices with Eisenstein integer entries forms a lattice in Minkowski spacetime, and I conjectured that $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$ consists exactly of the hexagon centers in the hexagonal tiling honeycomb — a highly symmetrical structure in hyperbolic space, discovered by Coxeter, which looks like this:

Now Greg Egan and I will prove that conjecture.

Last time, based on the work of Johnson and Weiss, we saw that the orientation-preserving symmetries of the hexagonal tiling honeycomb form the group $PGL(2,\mathbb{E})$. This is not only as an abstract isomorphism of groups: it’s an isomorphism of groups acting on hyperbolic space, where $GL(2,\mathbb{E})$ acts on $\mathfrak{h}_2(\mathbb{C})$ and its subset $\mathcal{H}$ by

$$g \colon A \mapsto g A g^\ast$$

and this action descends to the quotient $PGL(2,\mathbb{E})$.

By general abstract nonsense about Coxeter groups, the orientation-preserving symmetries of the hexagonal tiling honeycomb act transitively on the set of hexagon centers. Thus, if we choose a suitable point $p \in \mathcal{H}$, we can get all the hexagon centers by acting on this one. Then the set of hexagon centers is this:

$$\mathrm{Hex} = \{ g p g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \}$$

But what’s a suitable point $p$? I claim that the identity matrix will do, so

$$\mathrm{Hex} = \{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \}$$

Once we show this, we can study the set $\mathrm{Hex}$ in detail, allowing us to prove the result conjectured last time:

Theorem. $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H} = \mathrm{Hex}$, so the points in the lattice $\mathfrak{h}_2(\mathbb{E})$ that lie on the hyperboloid $\mathcal{H}$ are the centers of hexagons in a hexagonal tiling honeycomb.

But first things first: let’s see why the identity matrix can serve as a hexagon center!

The 12 hexagon centers closest to the identity

Suppose we take the identity as a hexagon center and get a bunch of points in hyperbolic space by acting on it by all possible transformations in $\mathrm{GL}(2,\mathbb{G})$. We get this set:

$$\mathrm{Hex} = \{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \}$$

But how do we know this is right? We need to check that the points in this set look like the hexagon centers in here:

with the identity smack dab in the middle.

As you can see from the picture, each hexagon center should have 12 nearest neighbors. But does it work that way for our proposed set $\mathrm{Hex}$? It will be enough to check that the identity matrix has 12 nearest neighbors in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$, and check that these 12 points are in $\mathrm{Hex}$. A symmetry argument then shows that each point in $\mathrm{Hex}$ has 12 nearest neighbors arranged in the same pattern, so the points in $\mathrm{Hex}$ are the centers of the hexagons in a hexagonal tiling honeycomb.

It’s easy to measure the distance to the identity matrix if you remember your hyperbolic trig. If we think of $\mathfrak{h}_2(\mathbb{C})$ as Minkowski spacetime by writing a point as

$$A = \left( \begin{array}{cc} t + z & x - i y \\ x + i y & t - z \end{array} \right)$$

then the time coordinate is $\mathrm{tr}(A)/2$. The distance in hyperbolic space from the identity to a point $A \in \mathcal{H}$ is then $\arccosh(\mathrm{tr}(A)/2)$.

But this is a monotonic function of $\mathrm{tr}(A)$. So let’s find the points $A \in \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$ with the smallest possible trace — not counting the identity itself, which has trace $2$. We hope there are 12.

Greg Egan found them:

and

where $k = 0,1,2,3,4,5$ and $\zeta = -\omega$. These matrices are the 6 magenta points and 6 yellow points shown here, while the black point is the identity:

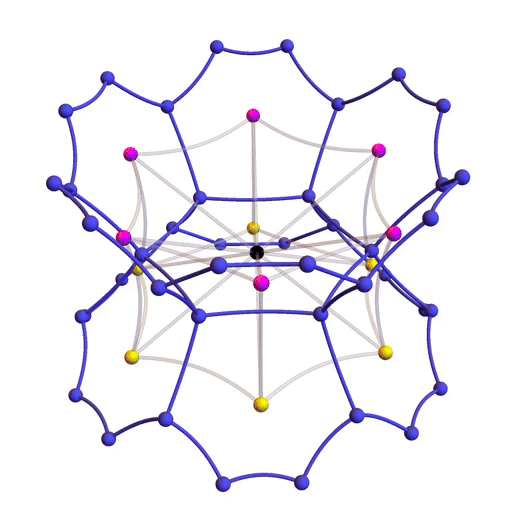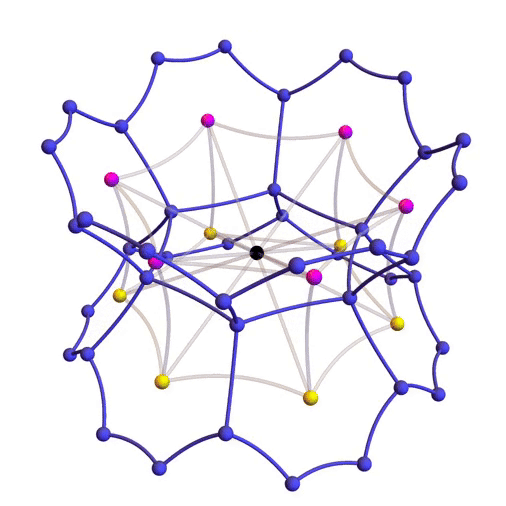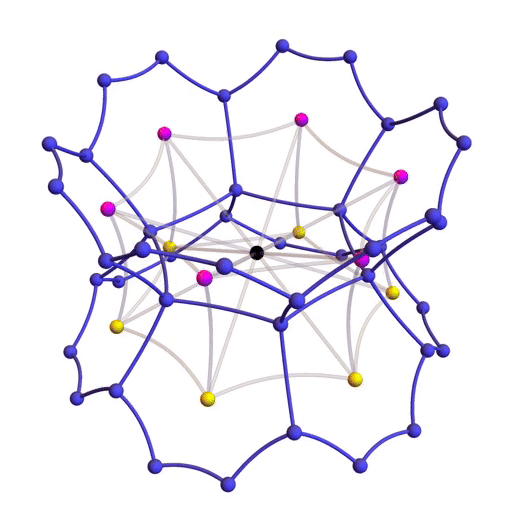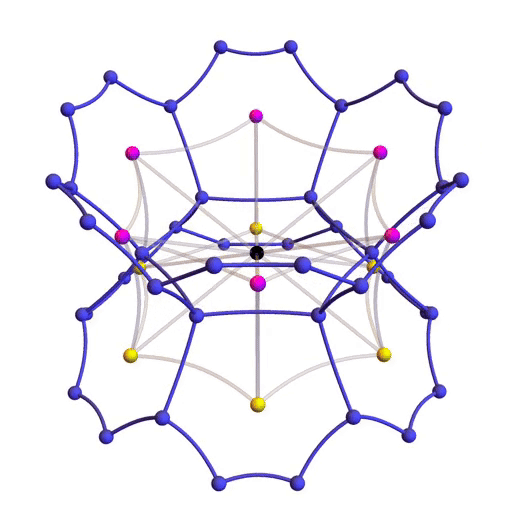
The dark blue points are hexagon vertices, which are not so important right now. By the way, the significance of $\zeta = -\omega$ is that it’s a primitive sixth root of unity; so is $\overline{\zeta}= \zeta^{-1}$. So these give the hexagonal pattern we seek.

These 12 matrices clearly lie in $\mathfrak{h}_2(\mathbb{E})$, and they have determinant $1$ and positive trace so they lie in $\mathcal{H}$. But the good part is this:

Lemma 1. The 12 matrices in equations (1) and (2) are the matrices in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$ that are as close as possible to the identity matrix without being equal to it. In other words, they have the smallest possible trace $\gt 2$ for matrices in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$.

I’ll put the proof of this and all the other lemmas in an appendix.

Now, why do these 12 matrices lie in

$$\mathrm{Hex} = \{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \} ?$$

Greg found 12 matrices $g \in \mathrm{GL}(2,\mathbb{E})$ that do the job, namely

$$u_k = \left( \begin{array}{cc} 1 & \zeta^k \\ 0 & 1 \\ \end{array} \right)$$

and

$$u_k^\ast = \left( \begin{array}{cc} 1 & 0 \\ \overline{\zeta}^k & 1 \\ \end{array} \right)$$

where $k = 0,1,2,3,4,5$.

A concrete construction of all the hexagon centers

Now we can get a concrete way to construct every element of the set

$$\mathrm{Hex} = \{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \}$$

Lemma 2. The group $\mathrm{SL}(2,\mathbb{E})$ consists of finite products of matrices of the form

$$u_k = \left( \begin{array}{cc} 1 & \zeta^k \\ 0 & 1 \\ \end{array} \right) \qquad \text{and} \qquad u_k^\ast = \left( \begin{array}{cc} 1 & 0 \\ \overline{\zeta}^k & 1 \\ \end{array} \right)$$

for $k = 0, 1, 2, 3, 4, 5$.

Lemma 3. Every element of $\mathrm{GL}(2,\mathbb{E})$ is an element of $\mathrm{SL}(2,\mathbb{E})$ multiplied on the right by some power of

$$h = \left( \begin{array}{cc} \zeta & 0 \\ 0 & 1 \\ \end{array} \right)$$

Notice that this element $h$ is in $\mathrm{GL}(2,\mathbb{E})$ but not in $\mathrm{SL}(2,\mathbb{E})$, and it acts on Minkowski space as a 60 degree rotation in the $x y$ plane, giving the rotational symmetry in Greg’s image:

While we can implement this 60 degree rotation with an element of $\mathrm{SL}(2,\mathbb{C})$, namely

$$\pm \left( \begin{array}{cc} \exp(2 \pi i / 12) & 0 \\ 0 & \exp(-2 \pi i / 12) \\ \end{array} \right)$$

we cannot do it with any element of $\mathrm{SL}(2,\mathbb{E})$. This is why we need to bring $\mathrm{GL}(2,\mathbb{E})$ into the game.

Lemma 4. The set $\mathrm{Hex}$ equals the set of matrices $g g^\ast$ where $g$ is a finite product of matrices of the form

$$u_k = \left( \begin{array}{cc} 1 & \zeta^k \\ 0 & 1 \\ \end{array} \right) \qquad \text{and} \qquad u_k^\ast = \left( \begin{array}{cc} 1 & 0 \\ \overline{\zeta}^k & 1 \\ \end{array} \right)$$

for $k = 0, 1, 2, 3, 4, 5$.

The theorem: first proof

Now we outline two proofs of the conjecture from last time. Greg did the hard part of the first proof, which uses some computer algebra we will only sketch. But the basic idea is this. We want to show that the points in the lattice $\mathfrak{h}_2(\mathbb{E})$ that lie on the hyperboloid $\mathcal{H}$ are precisely the centers of the hexagons in our hexagonal tiling honeycomb. It’s easy to show that all the hexagon centers lie in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$. The hard part is showing the converse. For this we assume we’ve got a point in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$ that’s not a hexagon center. We assume it’s as close as possible to the identity matrix. Then, we’ll find another such point that’s even closer — so no such point could exist.

Theorem. The points in the lattice $\mathfrak{h}_2(\mathbb{E})$ that lie on the hyperboloid $\mathcal{H}$ are precisely the centers of hexagons in a hexagonal tiling honeycomb, since

$$\mathrm{Hex} = \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$$

Proof. Part of this theorem is easy. Unfolding the definitions, we need to show

$$\{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \} = \{ A \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, \det(A) = 1, \; \mathrm{tr}(A) \gt 0 \}$$

But the only units in the Eisenstein integers are the 6th roots of unity, so for any $g \in \mathrm{GL}(2,\mathbb{E})$ its determinant is one of those, so $\det(g g^\ast) = 1$ and of course $\mathrm{tr}(g g^\ast) \gt 0$. This shows the set on the left-hand side is included in the set on the right-hand side.

So, the hard part is to show the reverse inclusion:

$$\{ A \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, \det(A) = 1, \; \mathrm{tr}(A) \gt 0 \} \subseteq \{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \}$$

By Lemma 4, it suffices to assume $A \in \mathfrak{h}_2(\mathbb{E})$ has $\det(A) = 1$ and $\mathrm{tr}(A) \gt 0$, and prove that $A$ is of the form $g g^\ast$, where $g$ is a finite product of matrices

$$u_k = \left( \begin{array}{cc} 1 & \zeta^k \\ 0 & 1 \\ \end{array} \right), \qquad \text{and} \qquad u^\ast_k = \left( \begin{array}{cc} 1 & 0 \\ \overline{\zeta}^k & 1 \\ \end{array} \right)$$

for $k = 0, 1, 2, 3, 4,$ or $5$.

For a contradiction, suppose there exists $A \in \mathfrak{h}_2(\mathbb{E})$ with $\det(A) = 1$ and $\mathrm{tr}(A) \gt 0$ that is not of this form. Since the set of such $A$ is discrete, we can choose one with the smallest possible trace. We now find one with a smaller trace, namely either $u_k A u^\ast_k$ or $u^\ast_k A u_k$ for some $k$.

We can write

$$A = \left( \begin{array}{cc} a & c+d \omega \\ (c-d)-d \omega & g \\ \end{array} \right)$$

for integers $a,c,d,g$ obeying the extra conditions:

$$\begin{array}{rcl} a+g &\gt&0 \\ a g-c^2+c d-d^2 &=&1 \end{array}$$

If we act on $A$ with each of the 12 elements $u_k, u^\ast_k \in \mathrm{SL}(2,\mathbb{E})$, the changes in the trace of the original matrix are linear expressions in either $a, c$ and $d$ or $g, c$ and $d$. It will only be impossible to reduce the trace if all 12 expressions are non-negative, for parameters where the determinant is 1.

It is easier to see what’s happening on a plot:

We would need to find values of $a$ and $g$ such that the green ellipse (the determinant condition) has a point with integer coordinates inside the smaller of the two hexagons (one of which scales with $a$, the other with $g$).

The shape of the ellipse and hexagons are such that if the ellipse passed through any one hexagon vertex it would pass through all of them.

We can write the changes in the trace as:

$$\begin{array}{rcl} \delta_k & = & \mathrm{tr}(u_k A u^\ast_k) - \mathrm{tr}(A) \\ & = & g + 2 c \cos \left(\frac{\pi k}{3}\right)+d \left(-\sqrt{3} \sin \left(\frac{\pi k}{3}\right)-\cos \left(\frac{\pi k}{3}\right)\right) \\ \Delta_k & = & \mathrm{tr}(u^\ast_k A u_k) - \mathrm{tr}(A) \\ & = & a + 2 c \cos \left(\frac{\pi k}{3}\right)+d \left(-\sqrt{3} \sin \left(\frac{\pi k}{3}\right)-\cos \left(\frac{\pi k}{3}\right)\right) \end{array}$$

Setting these to zero gives us the sides of the hexagons, while the vertices are found by solving:

$$\delta_k = \delta_{k+1} = 0$$

to obtain:

$$\begin{array}{rcl} c & = & \frac{1}{3} g \left(\sqrt{3} \sin \left(\frac{\pi k}{3}\right)-\cos \left(\frac{\pi k}{3}\right)\right) \\ d & = & \frac{2}{3} g \left(\cos \left(\frac{\pi k}{3}\right)-\cos \left(\frac{1}{3} \pi (k+1)\right)\right) \end{array}$$

The result for $\Delta_k$ is the same, but with $g$ replaced by $a$. Substituting these values into the formula for the determinant of $A$ and equating that to 1 gives us:

$$a g - \frac{g^2}{3} = 1$$

and for $\Delta_k$:

$$a g - \frac{a^2}{3} = 1$$

Without loss of generality we can assume $a \le g$, and use the curve defined by the second equation as the boundary for the region in the $(a,g)$ parameter space where the determinant ellipse contains points inside the $a$-hexagon. The plot below shows that this only happens for $a=g=1$, the identity matrix.

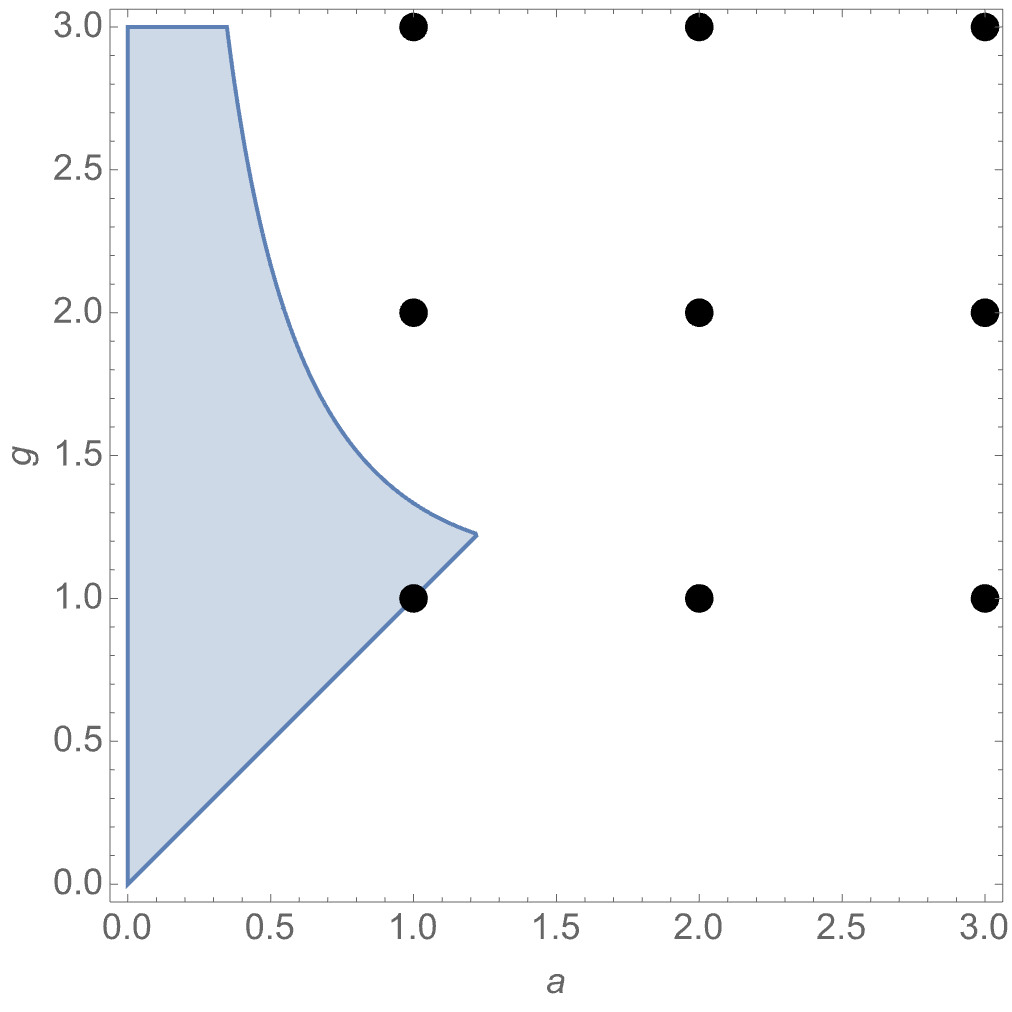
So, unless we are starting with the identity matrix, we can always act with one of the 12 elements $u_k, u^\ast_k \in \mathrm{SL}(2,\mathbb{E})$ and get an element with a smaller positive trace.       █

The theorem: second proof

After Greg gave the above proof on Mathstodon, Mist gave a different proof which uses more about Coxeter groups. In this approach, the argument that keeps reducing the trace of a purported counterexample is replaced by the standard fact that every Coxeter group acts transitively on the chambers of its Coxeter complex. I will quote their proof word for word.

Theorem. The points in the lattice $\mathfrak{h}_2(\mathbb{E})$ that lie on the hyperboloid $\mathcal{H}$ are precisely the centers of hexagons in a hexagonal tiling honeycomb, since

$$\mathrm{Hex} = \mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$$

Proof. Let me start with $\mathbb{R}^4$ with elements denoted $(t, x, y, z)$ and equipped with the negative of the Minkowski form, that is, $-t^2 + x^2 + y^2 + z^2$. Inside here, I choose vectors

$$\begin{array}{ccl} e_1 &=& (0, \frac{\sqrt{3}}{2}, \frac{1}{2}, 0) \\ e_2 &=& (0, -1, 0, 0) \\ e_3 &=& (\frac{1}{2}, \frac{1}{2}, -\frac{\sqrt{3}}{2}, \frac{1}{2}) \\ e_4 &=& (0, 0, 0, -1) \end{array}$$

By checking inner products, we see that these vectors and the aforementioned bilinear form determine a copy of the canonical representation of the rank-4 Coxeter group with diagram

$$\text{o--6--o-----o-----o}$$

where the 6 means that the edge is labeled ‘6’. My notation for the canonical representation is consistent with that of the Wikipedia article Coxeter complex.

By the general theory, the canonical representation acts transitively on the set of chambers, where the fundamental chamber is the tetrahedral cone cut out by the hyperplanes (through the origin) which are orthogonal to $e_1, e_2, e_3, e_4$. Direct computation (e.g. matrix inverse) shows us that the extremal rays of the fundamental chamber are given by the vectors

$$\begin{array}{c} (3, 0, -\sqrt{3}, 0) \\ (4, 1, -\sqrt{3}, 0) \\ (1, 0, 0, 0) \\ (1, 0, 0, 1) \end{array}$$

Here I have dropped constant factors, but one can (and perhaps should) normalize to ensure Minkowski norm 1. Now I check explicitly that these vectors match up with Greg’s earlier explicit description of “a portion of the honeycomb”:

• The vector $\frac{1}{\sqrt{6}}(3, 0, -\sqrt{3}, 0)$ is one of the blue vertices of the hexagon centered on the black point.
• The vector $(4, 1, -\sqrt{3}, 0)$ after normalization becomes the midpoint of the two blue vertices indexed by $k=0$ and $k=1$.
• The vector $(1, 0, 0, 0)$ is the identity matrix, i.e. the black point.
• The vector (1, 0, 0, 1) is the null vector for one of the two horospheres which contains the hexagon centered on the black point.

According to the Wikipedia article Hexagonal tiling honeycomb, the desired honeycomb is constructed from the aforementioned Coxeter group by applying the Wythoff construction with only the first vertex circled. This confirms that the hexagon centers correspond to the vector $(1, 0, 0, 0)$ and its images under the Coxeter group action.

It remains to show that the hexagon centers coincide with the elements of the Eisenstein lattice with Minkowski norm 1.

To show that the hexagon centers are contained in the Eisenstein lattice, it suffices to show that the Eisenstein lattice is invariant under the Coxeter group action. This follows by checking the action of each of the simple reflections:

$$v \mapsto v - 2 \langle v, e_i \rangle e_i.$$

In more detail, for $e_1$, the inner product $\langle v, e_1\rangle$ is a half-integer if $v$ is in the Eisenstein lattice, and the claim follows because $e_1$ is in the Eisenstein lattice. The same statement applies for $e_2$ and $e_4$, and ‘half-integer’ can even replaced by ‘integer.’ For $e_3$, the inner product $\langle v, e_3\rangle$ is an integer multiple of $\sqrt(3)/2$, and the claim follows because $\sqrt{3} e_3$ is in the Eisenstein lattice.

To show that the elements of the Eisenstein lattice with Minkowski norm $1$ are hexagon centers, it suffices to show this statement within the fundamental chamber. Let $n := (1, 0, 0, 1)$ be the null vector from before. Observe the following: - If $v$ lies in the forward light cone, i.e. $\mathrm{norm}(v) \gt 0$ and $t \gt 0$, then $\langle v, n\rangle \gt 0$. - If $v$ lies in the Eisenstein lattice, then $\langle v, n\rangle$ is an integer. - If $v$ lies in the fundamental chamber and satisfies $\mathrm{norm}(v) = 1$, then $\langle v, n\rangle \lt 2$. (Sketch: Restricting to $\mathrm{norm}(v) = 1$ gives hyperbolic geometry, and the interior-of-horosphere $\langle v, n \rangle \lt 2$ is convex, so it suffices to check the special cases when $v$ is a vertex of the fundamental chamber.) These observations imply that, if $v$ is an element of the Eisenstein lattice with $\mathrm{norm}(v) = 1$ lying in the fundamental chamber, then $\langle v, n \rangle = 1$.

Next, write $v = (t, x, y, z)$. Since$\langle v, n \rangle = 1$ rewrites as $t - z = 1$, the relation $\textrm{norm}(v) = 1$ rewrites as $x^2 + y^2 = 2z$. This tells us that the elements of the Eisenstein lattice with $\mathrm{norm}(v) = 1$ and $\langle v, n\rangle = 1$ are in bijection with the Eisenstein integers via

$$x + i y \; corresponds \; to \; ((x^2 + y^2)/2 + 1, x, y, (x^2 + y^2)/2) .$$

It is easy to check that the simple reflections $e_1, e_2, e_3$ preserve the aforementioned set of vectors $v$ and this bijection intertwines those simple reflections with the usual reflection symmetries of the Eisenstein integers (viewed as the vertices of the equilateral triangle lattice). Therefore, all of the aforementioned vectors v can be brought to $(1, 0, 0, 0)$ via a Coxeter group action, as desired.       █

What’s next?

A very similar theorem should be true for another regular hyperbolic honeycomb, the square tiling honeycomb:

Here instead of the Eisenstein integers we should use the Gaussian integers, $\mathbb{G}$, consisting of all complex numbers $a + b i$ with $a, b \in \mathbb{Z}$.

Conjecture. The points in the lattice $\mathfrak{h}_2(\mathbb{G})$ that lie on the hyperboloid $\mathcal{H}$ are the centers of squares in a square tiling honeycomb.

I’m also very interested in how these results connect to algebraic geometry! That’s the real theme of this series, and I discussed the connection last time. Briefly, the hexagon centers in the hexagonal tiling honeycomb correspond to principal polarizations of the abelian variety $\mathbb{C}^2/\mathbb{E}^2$. These are concepts that algebraic geometers know and love. Similarly, if the conjecture above is true, the square centers in the square tiling honeycomb will correspond to principal polarizations of the abelian variety $\mathbb{C}^2/\mathbb{G}^2$. But I’m especially interested in interpreting the other features of these honeycombs — not just the hexagon and square centers — using ideas from algebraic geometry.

Proofs of lemmas

Lemma 1. The 12 matrices

$$\left( \begin{array}{cc} 2 & \zeta^k \\ \overline{\zeta}^k & 1 \\ \end{array} \right) , \qquad \left( \begin{array}{cc} 1 & \zeta^k \\ \overline{\zeta}^k & 2 \\ \end{array} \right) \qquad \qquad k = 0,1,2,3,4,5$$

are the points in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$ that as close as possible to the identity matrix without being equal to it. In other words, they have the smallest possible trace $\gt 2$ for matrices in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$.

Proof. Matrices in $\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}$ are of the form

$$A = \left( \begin{array}{cc} t + z & x - i y \\ x + i y & t - z \end{array} \right)$$

where $t + z, t - z \in \mathbb{Z}$, $x + i y \in \mathbb{E}$, the trace $2t$ is $\gt 0$ and the determinant $t^2 - z^2 - |x + i y|^2$ is $1$. Since $t + z$ and $t - z$ are integers, $t$ and $z$ must be integers divided by 2.

The smallest possible trace for such a matrix is $2$, realized only by the identity matrix. We are looking at the second smallest possible trace, which is $3$. So, we have $t = 3/2$ and $t^2 - z^2 - |x + i y|^2 = 1$, i.e. $z^2 + |x + i y|^2 = 5/4$. Since $z$ is a half-integer and $x + i y$ is an Eisenstein integer, the only options are to let $z = \pm \frac{1}{2}$ and let $x + i y$ be an Eisenstein integer of norm $1$, i.e. a sixth root of unity. These give the matrices

$$\left( \begin{array}{cc} 2 & \zeta^k \\ \overline{\zeta}^k & 1 \\ \end{array} \right) , \qquad \left( \begin{array}{cc} 1 & \zeta^k \\ \overline{\zeta}^k & 2 \\ \end{array} \right)$$

for $k = 0,1,2,3,4,5$.       █

Lemma 2. The group $\mathrm{SL}(2,\mathbb{E})$ consists of finite products of matrices of the form

$$u_k = \left( \begin{array}{cc} 1 & \zeta^k \\ 0 & 1 \\ \end{array} \right) \qquad \text{and} \qquad u^\ast_k = \left( \begin{array}{cc} 1 & 0 \\ \overline{\zeta}^k & 1 \\ \end{array} \right)$$

for $k = 0, 1, 2, 3, 4, 5$.

Proof. In Section 8 of Quadratic integers and Coxeter groups, Johnson and Weiss cite Bianchi to say that $\mathrm{SL}(2,\mathbb{E})$ is generated by these matrices:

$$\left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right), \qquad \left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \end{array} \right) , \qquad \left( \begin{array}{cc} 1 & 0 \\ \omega & 1 \\ \end{array} \right)$$

The second and third of these matrices equal $u^\ast_0$ and $u^\ast_2$, respectively, so we just need to write the first,

$$\left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right),$$

as a product of matrices $u_k$ and $u^\ast_k$ (or their inverses, which are again matrices of this form). Since

$$\left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \\ \end{array} \right) = \left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right) \left( \begin{array}{cc} 0 & -1 \\ 1 & 1 \\ \end{array} \right)$$

we have

$$\left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right) = \left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \\ \end{array} \right) \left( \begin{array}{cc} 0 & -1 \\ 1 & 1 \\ \end{array} \right)^{-1}$$

Since the first matrix in this product is $u_0$, it suffices to note that

$$\left( \begin{array}{cc} 0 & -1 \\ 1 & 1 \\ \end{array} \right) = \left( \begin{array}{cc} 1 & -1 \\ 0 & 1 \\ \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \end{array} \right)$$ is the product of $u_3$ and $u^\ast_0$.       █

Lemma 3. Every element of $\mathrm{GL}(2,\mathbb{E})$ is an element of $\mathrm{SL}(2,\mathbb{E})$ multiplied on the right by some power of

$$h = \left( \begin{array}{cc} \zeta & 0 \\ 0 & 1 \\ \end{array} \right)$$

Proof. The determinant of any $g \in \mathrm{GL}(2,\mathbb{E})$ is some sixth root of unity, and the determinant of $h$ is a primitive sixth root of unity, so for some power $h^k$ we have $\det(g h^k) = 1$ and thus $g h^k\in \mathrm{SL}(2,\mathbb{E})$. It follows that $g$ equals some element of $\mathrm{SL}(2,\mathbb{E})$, namely $g h^k$, multiplied on the left by some power of $h$, namely $h^{-k}$.       █

Lemma 4. The set $\mathrm{Hex} = \{ g g^\ast \in \mathfrak{h}_2(\mathbb{E}) \, \vert \, g \in \mathrm{GL}(2,\mathbb{E}) \}$ equals the set of matrices $g g^\ast$ where $g$ is a finite product of the matrices $u_k$ and $u^\ast_k$.

Proof. By Lemma 3, $\mathrm{Hex}$ is exactly the set of matrices $(g h^k) (g h^k)^\ast$ where $g \in \mathrm{SL}(2,\mathbb{E})$ and

$$h = \left( \begin{array}{cc} \zeta & 0 \\ 0 & 1 \\ \end{array} \right)$$

But the adjoint of $h$ is its inverse so

$$(g h^k) (g h^k)^\ast = g h^k (h^k)^\ast g = g g^\ast$$

Thus, by Lemma 2, $\mathrm{Hex}$ is exactly the set of matrices $g g^\ast$ where $g$ is a finite product of the matrices $u_k$ and $u^\ast_k$.       █

I posted a link last week to a dialogue written by a former colleague of mine, Sylvain Ribault. Sylvain’s dialogue is a summary of different perspectives on academic publishing. Unlike certain more famous dialogues written by physicists, Sylvain’s account doesn’t have a clear bias: he’s trying to set out the concerns different stakeholders might have and highlight the history of the subject, without endorsing one particular approach as the right one.

The purpose of such a dialogue is to provoke thought, and true to its purpose, the dialogue got me thinking.

Why do peer review? Why do we ask three or so people to read every paper, comment on it, and decide whether it should be published? While one can list many reasons, they seem to fall into two broad groups:

1. We want to distinguish better science from worse science. We want to reward the better scientists with jobs and grants and tenure. To measure whether scientists are better, we want to see whether they publish more often in the better journals. We then apply those measures on up the chain, funding universities more when they have better scientists, and supporting grant programs that bring about better science.
2. We want published science to be true. We want to make sure that when a paper is published that the result is actually genuine, free both from deception and from mistakes. We want journalists and the public to know which scientific results are valid, and we want scientists to know what results they can base their own research on.

The first set of goals is a product of scarcity. If we could pay every scientist and fund every scientific project with no cost, we wouldn’t need to worry so much about better and worse science. We’d fund it all and see what happens. The second set of goals is more universal: the whole point of science is to find out the truth, and we want a process that helps to achieve that.

My approach to science is to break problems down. What happens if we had only the second set of concerns, and not the first?

Well, what happens to hobbyists?

I’ve called hobby communities a kind of “post-scarcity academia”. Hobbyists aren’t trying to get jobs doing their hobby or get grants to fund it. They have their day jobs, and research their hobby as a pure passion project. There isn’t much need to rank which hobbyists are “better” than others, but they typically do care about whether what they write is true. So what happens when it’s not?

Sometimes, not much.

My main hobby community was Dungeons and Dragons. In a game with over 50 optional rulebooks covering multiple partially compatible-editions, there were frequent arguments about what the rules actually meant. Some were truly matters of opinion, but some were true misunderstandings, situations where many people thought a rule worked a certain way until they heard the right explanation.

One such rule regarded a certain type of creature called a Warbeast. Warbeasts, like Tolkien’s Oliphaunts, are “upgraded” versions of more normal wild animals, bred and trained for war. There were rules to train a Warbeast, and people interpreted these rules differently: some thought you could find an animal in the wild and train it to become a Warbeast, others thought the rules were for training a creature that was already a Warbeast to fight.

I supported the second interpretation: you can train an existing Warbeast, you can’t train a wild animal to make it into a Warbeast. As such, keep in mind, I’m biased. But every time I explained the reasoning (pointing out that the text was written in the context of an earlier version of the game, and how the numbers in it matched up with that version), people usually agreed with me. And yet, I kept seeing people use the other interpretation. New players would come in asking how to play the game, and get advised to go train wild animals to make them into Warbeasts.

Ok, so suppose the Dungeons and Dragons community had a peer review process. Would that change anything?

Not really! The wrong interpretation was popular. If whoever first proposed it got three random referees, there’s a decent chance none of them would spot the problem. In good science, sometimes the problems with an idea are quite subtle. Referees will spot obvious issues (and not even all of those!), but only the most diligent review (which sometimes happens in mathematics, and pretty much nowhere else) can spot subtle flaws in an argument. For an experiment, you sometimes need more than that: not just a review, but an actual replication.

What would have helped the Dungeons and Dragons community? Not peer review, but citations.

Suppose that, every time someone suggested you could train a wild animal to make it a Warbeast, they had to link to the first post suggesting you could do this. Then I could go to that first post, and try to convince the author that my interpretation was correct. If I succeeded, the author could correct their post, and then every time someone followed one of these citation links it would tell them the claim was wrong.

Academic citations don’t quite work like this. But the idea is out there. People have suggested letting anyone who wants to review a paper, and publishing the reviews next to the piece like comments on a blog post. Sylvain’s dialogue mentions a setup like this, and some of the risks involved.

Still, a setup like that would have gone a long way towards solving the problem for the Dungeons and Dragons community. It has me thinking that something like that is worth exploring.

One of the biggest condensed matter trends in recent years has been the stacking of 2D materials and the development of moiré lattices.  The idea is, take a layer of 2D material and stack it either (1) on itself but with a twist angle, or (2) on another material with a slightly different lattice constant.  Because of interactions between the layers, the electrons in the material have an effective potential energy that has a spatial periodicity associated with the moiré pattern that results.  Twisted stacking hexagonal lattice materials (like graphene or many of the transition metal dichalcogenides) results in a triangular moiré lattice with a moiré lattice constant that depends on twist angle.  Some of the most interesting physics in these systems seems to pop out when the moiré lattice constant is on the order of a few nm to 10 nm or so.  The upside of the moiré approach is that it can produce such an effective lattice over large areas with really good precision and uniformity (provided that the twist angle can really be controlled - see here and here, for example.)  You might imagine using lithography to make designer superlattices, but getting the kind of cleanliness and homogeneity at these very small length scales is very challenging.

It's not surprising, then, that people are interested in somehow applying superlattice potentials to nearby monolayer systems.  Earlier this year, Nature Materials ran three papers published sequentially in one issue on this topic, and this is the accompanying News and Views article.

• In one approach, a MoSe2/WS2 bilayer is made and the charge in the bilayer is tuned so that the bilayer system is a Mott insulator, with charges localized in exactly the moiré lattice sites.  That results in an electrostatic potential that varies on the moiré lattice scale that can then influence a nearby monolayer, which then shows cool moiré/flat band physics itself.
• Closely related, investigators used a small-angle twisted bilayer of graphene.  That provides a moiré periodic dielectric environment for a nearby single layer of WSe2.  They can optically excite Rydberg excitons in the WSe2, excitons that are comparatively big and puffy and thus quite sensitive to their dielectric environment.  
• Similarly, twisted bilayer WS2 can be used to apply a periodic Coulomb potential to a nearby bilayer of graphene, resulting in correlated insulating states in the graphene that otherwise wouldn't be there.

Clearly this is a growth industry.  Clever, creative ways to introduce highly ordered superlattice potentials on very small lengthscales with other symmetries besides triangular lattices would be very interesting.

You thought this series was dead. But it was only dormant!

In Part 1, I explained how the classification of holomorphic line bundles on a complex torus $X$ breaks into two parts:

• the ‘discrete part’: their underlying topological line bundles are classified by elements of a free abelian group called the Néron–Severi group $\mathrm{NS}(X)$.

• the ‘continuous part’: the holomorphic line bundles with a given underlying topological line bundle are classified by elements of a complex torus called the Jacobian $\mathrm{Jac}(X)$.

In Part 2, I explained duality for complex tori, which is a spinoff of duality for complex vector spaces. I used this to give several concrete descriptions of the Néron–Severi group $NS(X)$.

But the fun for me lies in the examples. Today let’s actually compute a Néron–Severi group and begin seeing how it leads to this remarkable picture by Roice Nelson:

This is joint work with James Dolan.

The most interesting complex tori are the complex abelian varieties. These are not just complex manifolds: they’re projective varieties, so the ideas of algebraic geometry apply! To be precise, a complex abelian variety is an abelian group object in the category of smooth complex projective varieties.

If you want to learn the general theory, I recommend this:

• Christina Birkenhake and Herbert Lange, Complex Abelian Varieties, Springer, Berlin, 2013.

It’s given me more pleasure than any book I’ve read for a long time. One reason is that it ties the theory nicely to ideas from physics, like the Heisenberg group and — without coming out and saying so — geometric quantization. Another is that abelian varieties are a charming, safe playground for beginners in algebraic geometry. You can easily compute things, classify things, and so on. It really amounts to linear algebra where all your vector spaces have lattices in them.

But instead of talking about general theorems, I’d like to look at an interesting example.

Every 1-dimensional complex torus can be made into an abelian variety: 1-dimensional abelian varieties are called elliptic curves, and everyone loves them. In higher dimensions the story is completely different: most complex tori can’t be made into abelian varieties! So, a lot of interesting phenomena are first seen in dimension 2. 2-dimensional abelian varieties are called complex abelian surfaces.

Here’s a cheap way to get our hands on an abelian surface: take the product of two elliptic curves. It’s tempting to use one of the two most symmetrical elliptic curves:

• The Gaussian curve $\mathbb{C}/\mathbb{G}$, where

$$\mathbb{G} = \{ a + b i \; \vert \; a, b \in \mathbb{Z} \}$$

is called the ring of Gaussian integers because it’s the ring of algebraic integers in the field $\mathbb{Q}[i]$.

• The Eisenstein curve $\mathbb{C}/\mathbb{E}$, where

$$\mathbb{E} = \{ a + b \omega \; \vert \; a, b \in \mathbb{Z} \}$$

and $\omega$ is the cube root of unity $\exp(2 \pi i/ 3)$. $\mathbb{E}$ is called the ring of Eisenstein integers because its the ring of algebraic integers in the field $\mathbb{Q}[\omega]$.

The Gaussian integers form a square lattice:

while the Eisenstein integers form an equilateral triangular lattice:

There are no other lattices in the plane as symmetrical as these, though there are interesting runners-up coming from algebraic integers in other fields $\mathbb{Q}[\sqrt{-n}]$.

Since the Eisenstein curve has 6-fold symmetry while the Gaussian curve has only 4-fold symmetry, let’s go all out and form an abelian surface by taking a product of two copies of the Eistenstein curve! I’ll call it the Eisenstein surface:

$$E = \mathbb{C}/\mathbb{E} \times \mathbb{C}/\mathbb{E} = \mathbb{C}^2/\mathbb{E}^2$$

What are the symmetries of this? Like any complex torus, it acts on itself by translations. These are incredibly important, but they don’t preserve the group structure because they move the origin around. When we talk about morphisms of abelian varieties, we usually mean maps of varieties that also preserve the group structure. So what are the automorphisms of $E$ as an abelian variety?

Well, actually it’s nice to think about endomorphisms of $E$ as an abelian variety. Suppose $T \in \mathrm{M}_2(\mathbb{E})$ is any $2 \times 2$ matrix of Eisenstein integers. Then $T$ acts on $\mathbb{C}^2$ in a linear way, by matrix multiplication. It obviously maps the lattice $\mathbb{E}^2 \subset \mathbb{C}^2$ to itself. So it defines an endomorphism of $\mathbb{C}^2/\mathbb{E}^2$. In other words, it gives an endomorphism of the Eisenstein surface as an abelian variety!

It’s not hard to see that these are all we get. So

$$\mathrm{End}(E) = \mathrm{M}_2(\mathbb{E})$$

Note that these endomorphisms form a ring: not only can you multiply them (i.e. compose them), you can also add them pointwise. Indeed any abelian variety has a ring of endomorphisms for the same reason, and these rings are very important in the overall theory.

Among the endomorphisms are the automorphisms, and I believe the automorphism group of the Eisenstein surface is

$$\mathrm{Aut}(E) = \mathrm{GL}(2,\mathbb{E})$$

This is an infinite group because it contains ‘shears’ like

$$\left( \begin{matrix} 1 & 1 \\ 0 & 1 \end{matrix} \right)$$

Now, what about line bundles on the Eisenstein surface $E$? Let’s sketch how to figure out its Néron–Severi group $NS(E)$. Remember, this is a coarse classification of holomorphic line bundles where two count as the same if they are topologically isomorphic. Thus we get a discrete classification, not a ‘moduli space’.

I described the Néron–Severi group in a bunch of ways in Part 2. Here’s the one we want now. If $X$ is a complex torus we can write

$$X = V/L$$

where $V$ is a finite-dimensional complex vector space and $L$ is a lattice in $V$. The vector space $V$ has a dual $V^\ast$, defined in the usual way, and the lattice $L \subset V$ also has a dual $L^\ast \subset V^\ast$, defined in a different way:

$$L^\ast = \{ f \colon V \to \mathbb{R} : f \; is\; real&#8211;linear \; and\; f(v) \in \mathbb{Z} \; for \; all \; v \in L \}$$

Then we saw something I called Theorem $2'$:

Theorem $2'$. The Néron–Severi group $NS(X)$ consists of linear maps $h \colon V \to V^\ast$ that map $L$ into $L^\ast$ and have $h^\ast = h$.

The point here is that any linear map $f \colon V \to W$ has an adjoint $f^\ast \colon W^\ast \to V^\ast$, so the map $h$ has an adjoint $h^\ast \colon V^{\ast\ast} \to V^\ast$, but the double dual of $V$ is canonically isomorphic to $V$ itself, so with a nod and a wink we can write $h^\ast \colon V \to V^\ast$, so it makes sense to say $h^\ast = h$.

You may be slightly dazed now — are you seeing stars? Luckily, all of this becomes less confusing in our actual example where $V = \mathbb{C}^2$ and $L = \mathbb{E}^2$, since the standard inner product on $\mathbb{C}^2$ lets us identify this vector space with its dual, and — check this out, this part is not quite trivial — that lets us identify the lattice $\mathbb{E}$ with its dual!

So, the Neron–Severi group $NS(E)$ of the Eisenstein surface $E = \mathbb{C}^2/\mathbb{E}^2$ consists of $2 \times 2$ complex matrices that map $\mathbb{E}^2$ to itself and are self-adjoint!

But it’s even simpler than that, since $2 \times 2$ complex matrices that map $\mathbb{E}^2$ to itself are just $2 \times 2$ matrices of Eisenstein integers. The set of these is our friend $\mathrm{M}_2(\mathbb{E})$. But now we want the self-adjoint ones. I’ll denote the set of these by $\mathfrak{h}_2(\mathbb{E})$. Here the gothic $\mathfrak{h}$ stands for ‘hermitian’.

So we’ve figured out the Neron–Severi group of the Eisenstein surface. It consists of $2 \times 2$ hermitian matrices of Eisenstein integers:

$$NS(E) = \mathfrak{h}_2(\mathbb{E}) \; !$$

Now let’s try to visualize it.

The fun part

I’ll dig into this more next time, but let me state the marvelous facts now, just to whet your appetite. The space of all complex $2 \times 2$ self-adjoint matrices, called $\mathfrak{h}_2(\mathbb{C})$, is famous in physics. It’s 4-dimensional — and it’s a nice way of thinking about Minkowski spacetime, our model of spacetime in special relativity.

Sitting inside Minkowski spacetime, we now see the lattice $\mathfrak{h}_2(\mathbb{E})$ of $2 \times 2$ self-adjoint matrices with Eisenstein number entries. It’s a very nice discretization of spacetime.

It’s a bit hard to visualize 4-dimensional things. So let’s look at $2 \times 2$ self-adjoint matrices whose determinant is $1$ and whose trace is positive. These form a 3-dimensional hyperboloid in Minkowski spacetime, called hyperbolic space. And it’s no hyperbole to say that this a staggeringly beautiful alternative to 3-dimensional Euclidean space. It’s negatively curved, so lines that start out parallel get further and further apart in an exponential way as they march along. There’s a lot more room in hyperbolic space — a lot of room for fun.

What happens if we look at points in our lattice $\mathfrak{h}_2(\mathbb{E})$ that happen to lie in hyperbolic space? I believe we get the centers of the hexagons in this picture:

And I believe the other features of this picture arise from other relationships between $\mathfrak{h}_2(\mathbb{E})$ and hyperbolic space. There’s a lot to check here. Greg Egan has made a lot of progress, but I’ll talk about that next time.

One last thing. I showed you that elements of $\mathfrak{h}_2(\mathbb{E})$ correspond to topological isomorphism classes of holomorphic line bundles on the Eisenstein surface. Then I showed you a cool picture of a subset of $\mathfrak{h}_2(\mathbb{E})$, namely the elements with determinant $1$ and trace $&gt; 0$. But what’s the importance of these? Am I focusing on them merely to get a charismatic picture in hyperbolic space?

No: it turns out that these elements correspond to something really nice: principal polarizations of the Eisenstein surface! These come from very best line bundles, in a certain precise sense.

It has been extremely busy in the ten months or so since I last wrote something here. It’s perhaps the longest break I’ve taken from blogging for 20 years (gosh!) but I think it was a healthy thing to do. Many readers have been following some of my ocassional scribblings … Click to continue reading this post →

The post Living in the Matrix – Recent Advances in Understanding Quantum Spacetime appeared first on Asymptotia.

read more

Before this week’s post: a former colleague of mine from CEA Paris-Saclay, Sylvain Ribault, posted a dialogue last week presenting different perspectives on academic publishing. One of the highlights of my brief time at the CEA were the times I got to chat with Sylvain and others about the future forms academia might take. He showed me a draft of his dialogue a while ago, designed as a way to introduce newcomers to the debate about how, and whether, academics should do peer review. I’ve got a different topic this week so I won’t say much more about it, but I encourage you to take a look!

Matt Strassler has a nice post up about waves and particles. He’s writing to address a common confusion, between two concepts that sound very similar. On the other hand, there are the waves of quantum field theory, ripples in fundamental fields the smallest versions of which correspond to particles. (Strassler likes to call them “wavicles”, to emphasize their wavy role.) On the other hand, there are the wavefunctions of quantum mechanics, descriptions of the behavior of one or more interacting particles over time. To distinguish, he points out that wavicles can hurt you, while wavefunctions cannot. Wavicles are the things that collide and light up detectors, one by one, wavefunctions are the math that describes when and how that happens. Many types of wavicles can run into each other one by one, but their interactions can all be described together by a single wavefunction. It’s an important point, well stated.

(I do think he goes a bit too far in saying that the wavefunction is not “an object”, though. That smacks of metaphysics, and I think that’s not worth dabbling in for physicists.)

After reading his post, there’s something that might still confuse you. You’ve probably heard that in quantum mechanics, an electron is both a wave and a particle. Does the “wave” in that saying mean “wavicle”, or “wavefunction”?

The gif above shows data from a double-slit experiment, an important type of experiment from the early days of quantum mechanics. These experiments were first conducted before quantum field theory (and thus, before the ideas that Strassler summarizes with “wavicles”). In a double-slit experiment, particles are shot at a screen through two slits. The particles that hit the screen can travel through one slit or the other.

Classically, you would expect particles shot randomly at the screen to form two piles on the other side, one in front of each slit. Instead, they bunch up into a rippling pattern, the same sort of pattern that was used a century earlier to argue that light was a wave. The peaks and troughs of the wave pass through both slits, and either line up or cancel out, leaving the distinctive pattern.

When it was discovered that electrons do this too, it led to the idea that electrons must be waves as well, despite also being particles. That insight led to the concept of the wavefunction. So the “wave” in the saying refers to wavefunctions.

But electrons can hurt you, and as Strassler points out, wavefunctions cannot. So how can the electron be a wavefunction?

To risk a bit of metaphysics myself, I’ll just say: it can’t. An electron can’t “be” a wavefunction.

The saying, that electrons are both particles and waves, is from the early days of quantum mechanics, when people were confused about what it all meant. We’re still confused, but we have some better ways to talk about it.

As a start, it’s worth noticing that, whenever you measure an electron, it’s a particle. Each electron that goes through the slits hits your screen as a particle, a single dot. If you see many electrons at once, you may get the feeling that they look like waves. But every actual electron you measure, every time you’re precise enough to notice, looks like a particle. And for each individual electron, you can extrapolate back the path it took, exactly as if it traveled like a particle the whole way through.

The same is true, though, of light! When you see light, photons enter your eyes, and each one that you see triggers a chemical change in a molecule called a photopigment. The same sort of thing happens for photographs, while an electrical signal gets triggered instead in a digital camera. Light may behave like a wave in some sense, but every time you actually observe it it looks like a particle.

But while you can model each individual electron, or photon, as a classical particle, you can’t model the distribution of multiple electrons that way.

That’s because in quantum mechanics, the “paths not taken” matter. A single electron will only go through one slit in the double-slit experiment. But the fact that it could have gone through both slits matters, and changes the chance that it goes through each particular path. The possible paths in the wavefunction interfere with each other, the same way different parts of classical waves do.

That role of the paths not taken, of the “what if”, is the heart and soul of quantum mechanics. No matter how you interpret its mysteries, “what if” matters. If you believe in a quantum multiverse, you think every “what if” happens somewhere in that infinity of worlds. If you think all that matters is observations, then “what if” shows the folly of modeling the world as anything else. If you are tempted to try to mend quantum mechanics with faster-than-light signals, then you have to declare one “what if” the true one. And if you want to double-down on determinism and replace quantum mechanics, you need to declare that certain “what if” questions are off-limits.

“What if matters” isn’t the same as a particle traveling every path at once, it’s its own weird thing with its own specific weird consequences. It’s a metaphor, because everything written in words is a metaphor. But it’s a better metaphor than thinking an electron is both a particle and a wave.

A recent paper of Kra, Moreira, Richter, and Robertson established the following theorem, resolving a question of Erdös. Given a discrete amenable group , and a subset of , we define the Banach density of to be the quantity

Theorem 1 Let be a countably infinite abelian group with the index finite. Let be a positive Banach density subset of . Then there exists an infinite set and such that .

Strictly speaking, the main result of Kra et al. only claims this theorem for the case of the integers , but as noted in the recent preprint of Charamaras and Mountakis, the argument in fact applies for all countable abelian in which the subgroup has finite index. This condition is in fact necessary (as observed by forthcoming work of Ethan Acklesberg): if has infinite index, then one can find a subgroup of of index for any that contains (or equivalently, is -torsion). If one lets be an enumeration of , and one can then check that the set

Theorem 1 resembles other theorems in density Ramsey theory, such as Szemerédi’s theorem, but with the notable difference that the pattern located in the dense set is infinite rather than merely arbitrarily large but finite. As such, it does not seem that this theorem can be proven by purely finitary means. However, one can view this result as the conjunction of an infinite number of statements, each of which is a finitary density Ramsey theory statement. To see this, we need some more notation. Observe from Tychonoff’s theorem that the collection is a compact topological space (with the topology of pointwise convergence) (it is also metrizable since is countable). Subsets of can be thought of as properties of subsets of ; for instance, the property a subset of of being finite is of this form, as is the complementary property of being infinite. A property of subsets of can then be said to be closed or open if it corresponds to a closed or open subset of . Thus, a property is closed and only if if it is closed under pointwise limits, and a property is open if, whenever a set has this property, then any other set that shares a sufficiently large (but finite) initial segment with will also have this property. Since is compact and Hausdorff, a property is closed if and only if it is compact.

The properties of being finite or infinite are neither closed nor open. Define a smallness property to be a closed (or compact) property of subsets of that is only satisfied by finite sets; the complement to this is a largeness property, which is an open property of subsets of that is satisfied by all infinite sets. (One could also choose to impose other axioms on these properties, for instance requiring a largeness property to be an upper set, but we will not do so here.) Examples of largeness properties for a subset of include:

• has at least elements.
• is non-empty and has at least elements, where is the smallest element of .
• is non-empty and has at least elements, where is the element of .
• halts when given as input, where is a given Turing machine that halts whenever given an infinite set as input. (Note that this encompasses the preceding three examples as special cases, by selecting appropriately.)

-large set

Theorem 1 is then equivalent to the following “almost finitary” version (cf. this previous discussion of almost finitary versions of the infinite pigeonhole principle):

Theorem 2 (Almost finitary form of main theorem) Let be a countably infinite abelian group with finite. Let be a Følner sequence in , let , and let be a largeness property for each . Then there exists such that if is such that for all , then there exists a shift and contains a -large set such that .

Proof of Theorem 2 assuming Theorem 1. Let , , be as in Theorem 2. Suppose for contradiction that Theorem 2 failed, then for each we can find with for all , such that there is no and -large such that . By compactness, a subsequence of the converges pointwise to a set , which then has Banach density at least . By Theorem 1, there is an infinite set and a such that . By openness, we conclude that there exists a finite -large set contained in , thus . This implies that for infinitely many , a contradiction.

Proof of Theorem 1 assuming Theorem 2. Let be as in Theorem 1. If the claim failed, then for each , the property of being a set for which would be a smallness property. By Theorem 2, we see that there is a and a obeying the complement of this property such that , a contradiction.

Remark 3 Define a relation between and by declaring if and . The key observation that makes the above equivalences work is that this relation is continuous in the sense that if is an open subset of , then the inverse image

is also open. Indeed, if for some , then contains a finite set such that , and then any that contains both and lies in .

For each specific largeness property, such as the examples listed previously, Theorem 2 can be viewed as a finitary assertion (at least if the property is “computable” in some sense), but if one quantifies over all largeness properties, then the theorem becomes infinitary. In the spirit of the Paris-Harrington theorem, I would in fact expect some cases of Theorem 2 to undecidable statements of Peano arithmetic, although I do not have a rigorous proof of this assertion.

Despite the complicated finitary interpretation of this theorem, I was still interested in trying to write the proof of Theorem 1 in some sort of “pseudo-finitary” manner, in which one can see analogies with finitary arguments in additive combinatorics. The proof of Theorem 1 that I give below the fold is my attempt to achieve this, although to avoid a complete explosion of “epsilon management” I will still use at one juncture an ergodic theory reduction from the original paper of Kra et al. that relies on such infinitary tools as the ergodic decomposition, the ergodic theory, and the spectral theorem. Also some of the steps will be a little sketchy, and assume some familiarity with additive combinatorics tools (such as the arithmetic regularity lemma).

— 1. Proof of theorem —

The proof of Kra et al. proceeds by establishing the following related statement. Define a (length three) combinatorial Erdös progression to be a triple of subsets of such that there exists a sequence in such that converges pointwise to and converges pointwise to . (By , we mean with respect to the cocompact filter; that is, that for any finite (or, equivalently, compact) subset of , for all sufficiently large .)

Theorem 4 (Combinatorial Erdös progression) Let be a countably infinite abelian group with finite. Let be a positive Banach density subset of . Then there exists a combinatorial Erdös progression with and non-empty.

Let us see how Theorem 4 implies Theorem 1. Let be as in Theorem 4. By hypothesis, contains an element of , thus and . Setting to be a sufficiently large element of the sequence , we conclude that and . Setting to be an even larger element of this sequence, we then have and . Setting to be an even larger element, we have and . Continuing in this fashion we obtain the desired infinite set .

It remains to establish Theorem 4. The proof of Kra et al. converts this to a topological dynamics/ergodic theory problem. Define a topological measure-preserving -system to be a compact space equipped with a Borel probability measure as well as a measure-preserving homeomorphism . A point in is said to be generic for with respect to a Følner sequence if one has

Theorem 4 then follows from

Theorem 5 (Dynamical Erdös progression) Let be a countably infinite abelian group with finite. Let be a topological measure-preserving -system, let be a -generic point of for some Følner sequence , and let be a positive measure open subset of . Then there exists a dynamical Erdös progression with and .

Indeed, we can take to be , to be , to be the shift , , and to be a weak limit of the for a Følner sequence with , at which point Theorem 4 follows from Theorem 5 after chasing definitions. (It is also possible to establish the reverse implication, but we will not need to do so here.)

A remarkable fact about this theorem is that the point need not be in the support of ! (In a related vein, the elements of the Følner sequence are not required to contain the origin.)

Using a certain amount of ergodic theory and spectral theory, Kra et al. were able to reduce this theorem to a special case:

Theorem 6 (Reduction) To prove Theorem 5, it suffices to do so under the additional hypotheses that is ergodic, and there is a continuous factor map to the Kronecker factor. (In particular, the eigenfunctions of can be taken to be continuous.)

We refer the reader to the paper of Kra et al. for the details of this reduction. Now we specialize for simplicity to the case where is a countable vector space over a finite field of size equal to an odd prime , so in particular ; we also specialize to Følner sequences of the form for some and . In this case we can prove a stronger statement:

Theorem 7 (Odd characteristic case) Let for an odd prime . Let be a topological measure-preserving -system with a continuous factor map to the Kronecker factor, and let be open subsets of with . Then if is a -generic point of for some Følner sequence , there exists an Erdös progression with and .

Indeed, in the setting of Theorem 5 with the ergodicity hypothesis, the set has full measure, so the hypothesis of Theorem 7 will be verified in this case. (In the case of more general , this hypothesis ends up being replaced with ; see Theorem 2.1 of this recent preprint of Kousek and Radic for a treatment of the case (but the proof extends without much difficulty to the general case).)

As with Theorem 1, Theorem 7 is still an infinitary statement and does not have a direct finitary analogue (though it can likely be expressed as the conjunction of infinitely many such finitary statements, as we did with Theorem 1). Nevertheless we can formulate the following finitary statement which can be viewed as a “baby” version of the above theorem:

Theorem 8 (Finitary model problem) Let be a compact metric space, let be a finite vector space over a field of odd prime order. Let be an action of on by homeomorphisms, let , and let be the associated -invariant measure . Let be subsets of with for some . Then for any , there exist such that

Let us now give a finitary proof of Theorem 8. We can cover the compact metric space by a finite collection of open balls of radius . This induces a coloring function that assigns to each point in the index of the first ball that covers that point. This then induces a coloring of by the formula . We also define the pullbacks for . By hypothesis, we have , and it will now suffice by the triangle inequality to show that

Now we can prove the infinitary result in Theorem 7. Let us place a metric on . By sparsifying the Følner sequence , we may assume that the grow as fast as we wish. Once we do so, we claim that for each , we can find such that for each , there exists that lies outside of such that

Fix , and let be a large parameter (much larger than ) to be chosen later. By genericity, we know that the discrete measures converge vaguely to , so any point in the support in can be approximated by some point with . Unfortunately, does not necessarily lie in this support! (Note that need not contain the origin.) However, we are assuming a continuous factor map to the Kronecker factor , which is a compact abelian group, and pushes down to the Haar measure of , which has full support. In particular, thus pushforward contains . As a consequence, we can find such that converges to , even if we cannot ensure that converges to . We are assuming that is a coset of , so now converges vaguely to .

We make the random choice , , where is drawn uniformly at random from . This is not the only possible choice that can be made here, and is in fact not optimal in certain respects (in particular, it creates a fair bit of coupling between , ), but is easy to describe and will suffice for our argument. (A more appropriate choice, closer to the arguments of Kra et al., would be to in the above construction by , where the additional shift is a random variable in independent of that is uniformly drawn from all shifts annihilated by the first characters associated to some enumeration of the (necessarily countable) point spectrum of , but this is harder to describe.)